Question 5 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

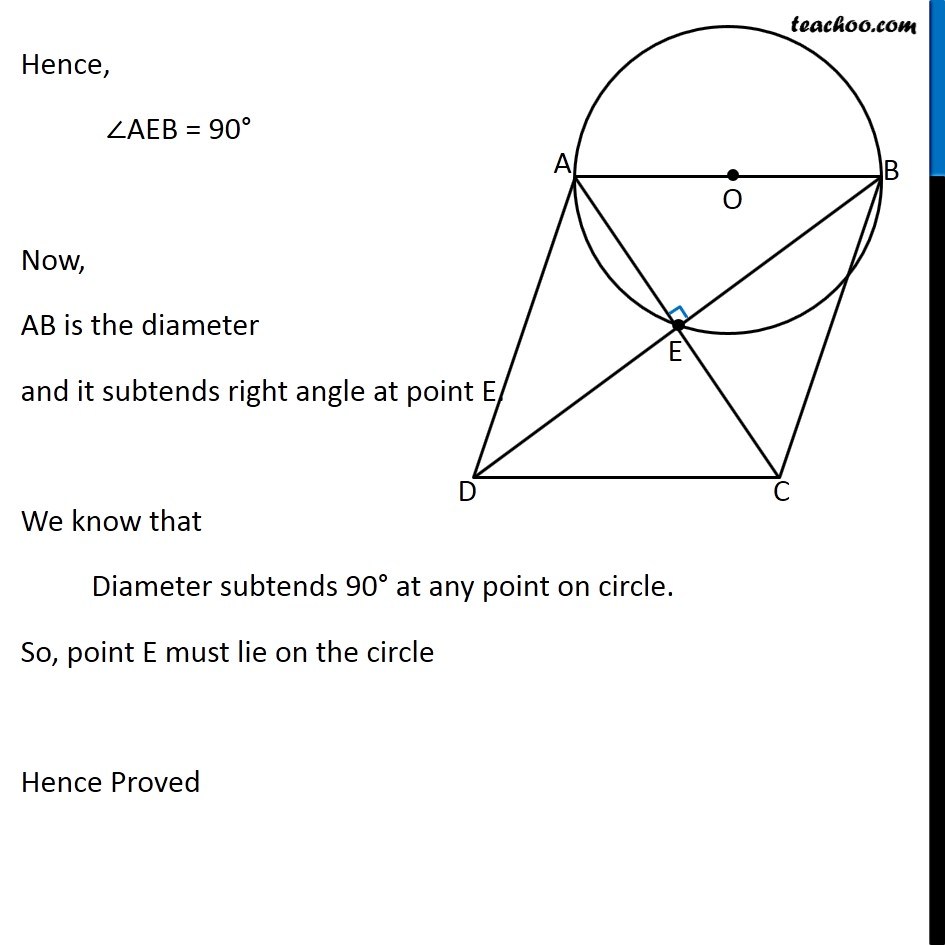
Question 5 Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonal. Given: Let ABCD be the rhombus and a circle is drawn taking AB as diameter To Prove: Point E lies on the circle Construction: Let point E be intersection of diagonals AC & BD Proof: We know that Diagonals of a rhombus bisect each other at right angles Hence, ∠AEB = 90° Now, AB is the diameter and it subtends right angle at point E. We know that Diameter subtends 90° at any point on circle. So, point E must lie on the circle Hence Proved