Question 7 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

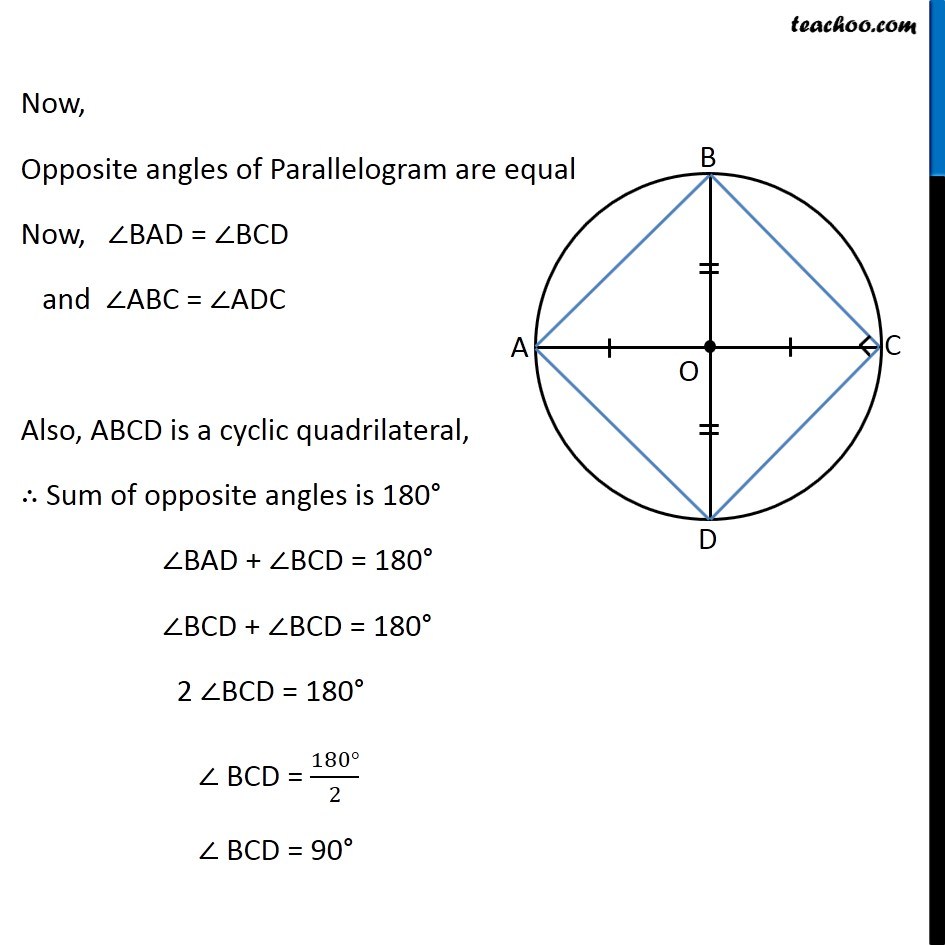
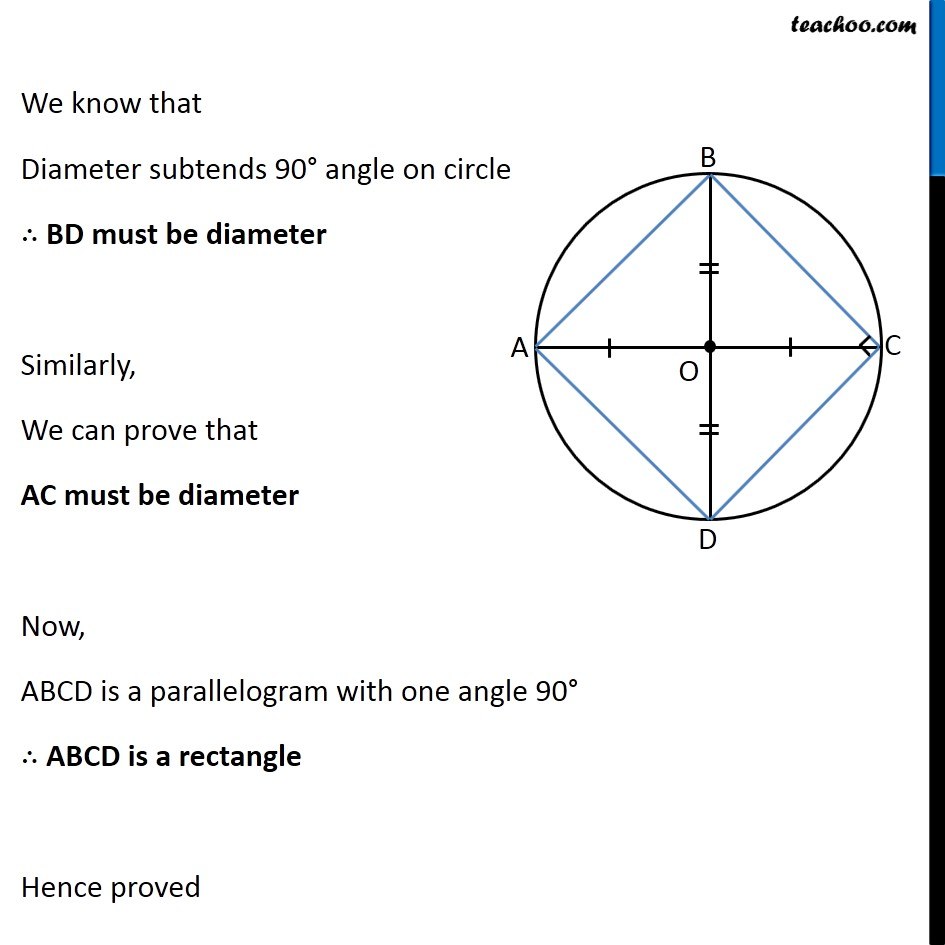
Question 7 AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle. Given: Chords AC and BD bisect each other To Prove: (i) AC and BD are diameters (ii) ABCD is a rectangle. Proof: In quadrilateral ABCD, AC bisects BD (given) So, diagonals bisect each other ∴ ABCD is a Parallelogram (In a parallelogram, diagonals bisect each other) Now, Opposite angles of Parallelogram are equal Now, ∠BAD = ∠BCD and ∠ABC = ∠ADC Also, ABCD is a cyclic quadrilateral, ∴ Sum of opposite angles is 180° ∠BAD + ∠BCD = 180° ∠BCD + ∠BCD = 180° 2 ∠BCD = 180° ∠ BCD = (180°)/2 ∠ BCD = 90° We know that Diameter subtends 90° angle on circle ∴ BD must be diameter Similarly, We can prove that AC must be diameter Now, ABCD is a parallelogram with one angle 90° ∴ ABCD is a rectangle Hence proved