Question 3 - Solving easy equations - Word Problems - Chapter 2 Class 8 Linear Equations in One Variable

Transcript

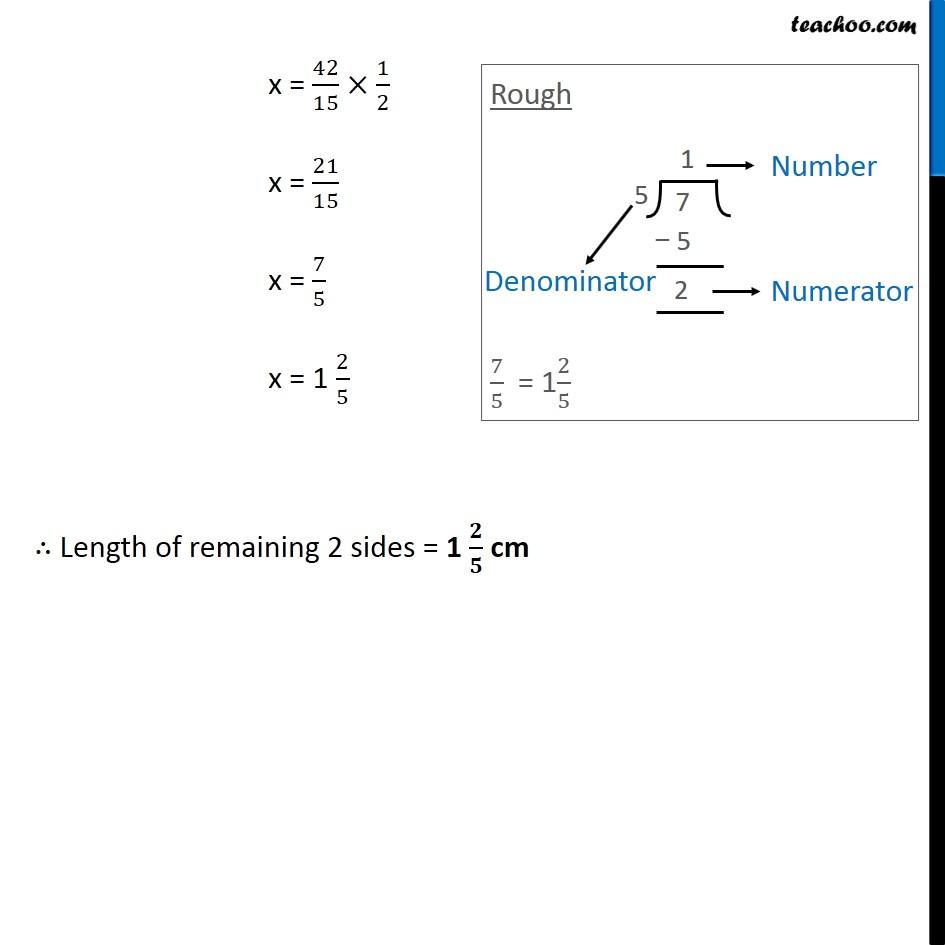
Question 3 The base of an isosceles triangle is 4/3 cm. The perimeter of the triangle is 4 2/15 cm. What is the length of either of the remaining equal sides? Let Δ ABC be an isosceles triangle Base = BC = 4/3 cm Let AB = x So BC = x (Two sides of an isosceles triangle are equal) Given, Perimeter = 4 2/15 cm = (4 × 15 + 2)/15 = (60 + 2)/15 = 62/15 Also, Perimeter = Sum of sides 62/15= AB + AC + BC 62/15= x + x + 4/3 62/15= 2x + 4/3 2x + 4/3 = 62/15 2x = 62/15− 4/3 2x = (62 − 4 × 5 )/15 2x = (62 − 20)/15 2x = 42/15 x = 42/15×1/2 x = 21/15 x = 7/5 x = 1 2/5 ∴ Length of remaining 2 sides = 1 𝟐/𝟓 cm Rough Converting 7/5 into mixed fraction 7/5 = 1 2/5