




Forming equations and solving
Last updated at Dec. 16, 2024 by Teachoo







Transcript
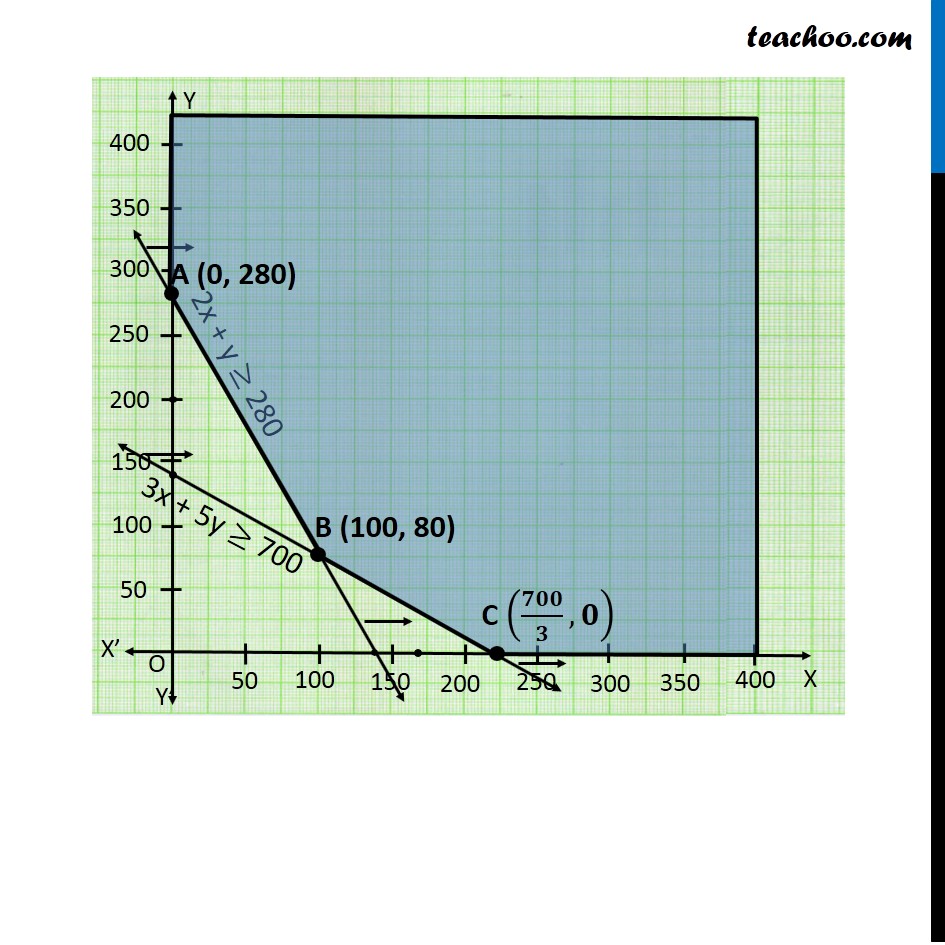
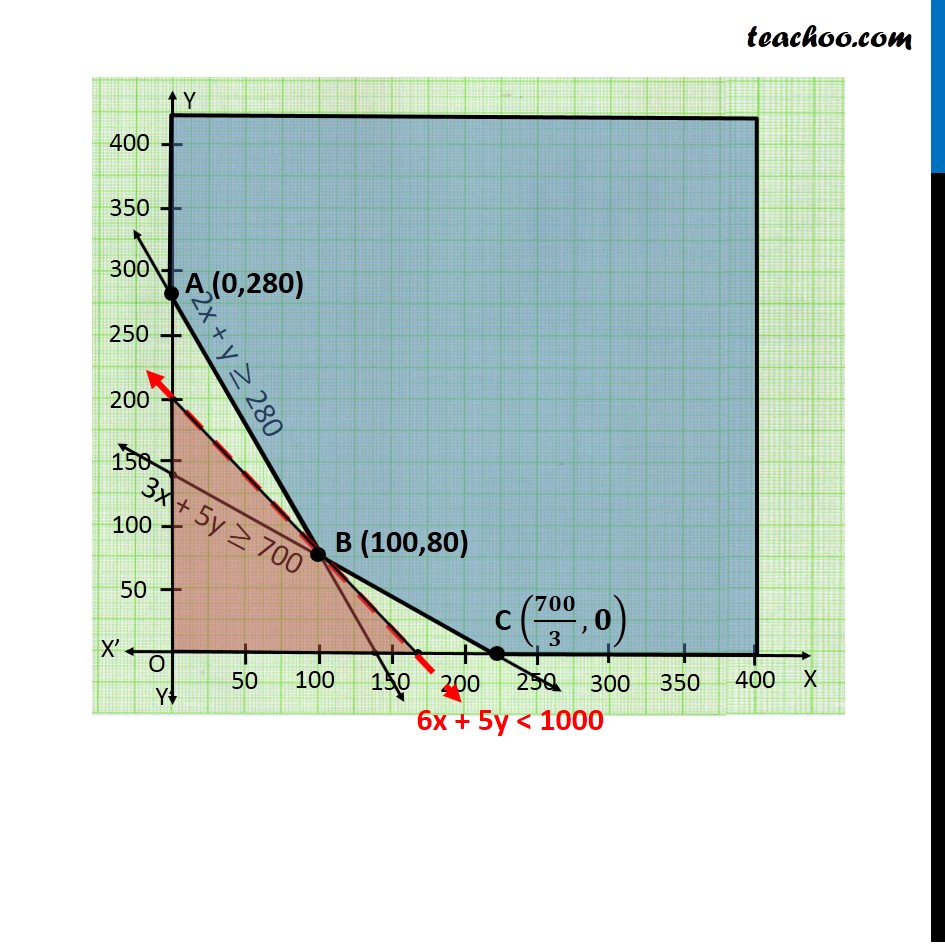
Question 10 There are two types of fertilisers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs Rs 6/kg and F2 costs Rs 5/kg, determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost? Let the fertilizer F1 requirement be x kg fertilizer F2 requirement be y kg According to Question : Nitrogen Quantity of Nitrogen in F1 = 10% Quantity of Nitrogen in F2 = 5% Minimum Available = 14 kg ∴ 10% of x + 5% of y ≥ 14 10/100 x + 5/100 y ≥ 14 2x + y ≥ 280 Phosphoric Acid Quantity of Acid in F1 = 6% Quantity of Acidin F2 = 10% Minimum Available = 14 kg ∴ 6% of x + 10% of y ≥ 14 6/100 x + 10/100 y ≥ 14 3x + 5y ≥ 700 As we need to Minimize the cost, hence the function used here is Minimize z. Cost of fertilizer F1 = Rs 6 k/g Cost of fertilizer F2 = Rs 5 k/g Minimize z = 6x + 5y Combining all Constraints : Min Z = 6x + 5y Subject to constraints 2x + y ≥ 280 3x + 5y ≥ 700 x, y ≥ 0 Since, there is no common point between the feasible region and 6x + 5y < 1000 Hence the cost will be minimum, if Fertilizer F1 used = 100 kg Fertilizer F2 used = 80 kg Minimum Cost = Rs 1000