Question 3 - Forming equations and solving - Chapter 12 Class 12 Linear Programming

Transcript

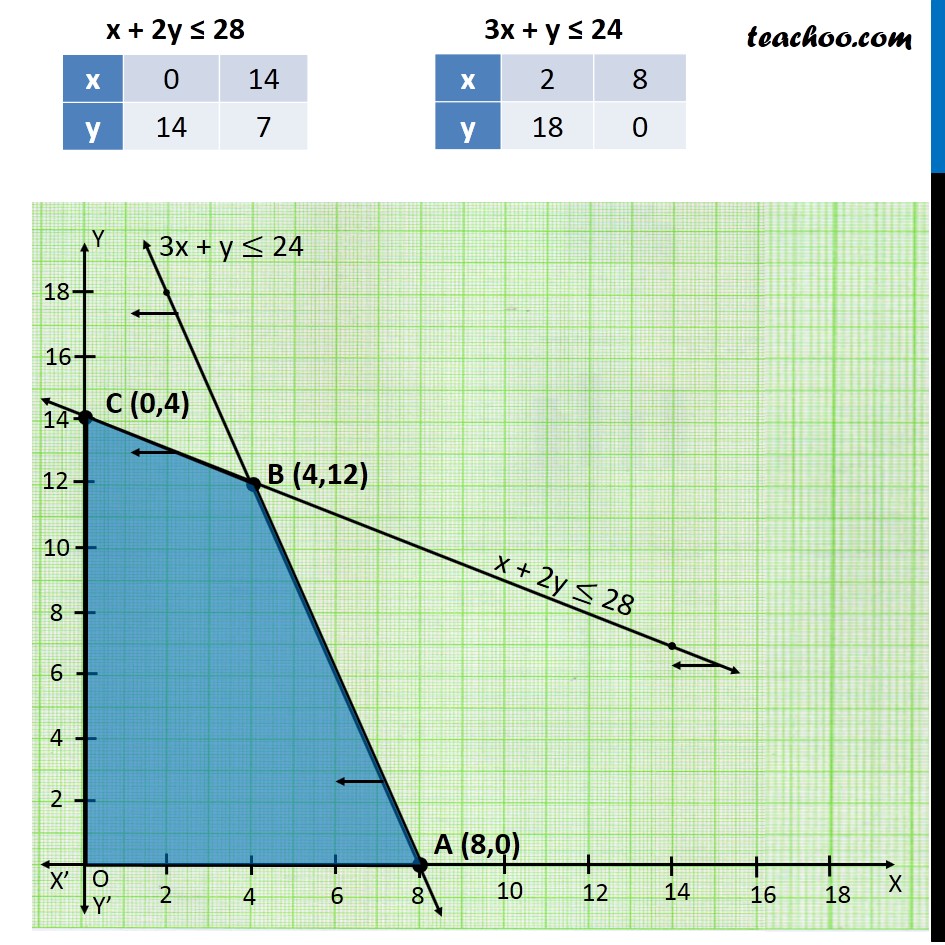
Question 3 A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time & 24 hours of craftsman’s time. (i) What number of rackets and bats must be made if the factory is to work at full capacity? (ii) If the profit on a racket & on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.Let Number of Tennis Racket be x Number of Cricket Bats be y According to Question : As we want Maximize the profit. Hence the function used here will be Maximize Z Machine Hours Tennis Racket requires → 1.5 hrs Cricket Bat requires → 3 hrs Max time available → 42 hrs ∴ 1.5x + 3y ≤ 42 3x + 6y ≤ 84 x + 2y ≤ 28 Craftsman's Hours Tennis Racket requires → 3 hrs Cricket Bat requires → 1 hrs Max time Available → 24 hrs ∴ 3x + y ≤ 24 Profit on each tennis racket → Rs 20 Profit on each Cricket Bat → Rs 10 ∴ Max Z = 20x + 10y Combining all the constraints : Maximize Z = 20x + 10y Subject to constraints, x + 2y ≤ 28 3x + y ≤ 24 x ≥ 0, y ≥ 0 x + 2y ≤ 28 3x + y ≤ 24 Thus, 4 Tennis Rackets and 12 Cricket Bats must be made so that factory runs at full capacity. Maximum Profit is Rs 200, when 4 tennis bats and 2 cricket bats are Produced.