Question 2 - Forming equations and solving - Chapter 12 Class 12 Linear Programming

Transcript

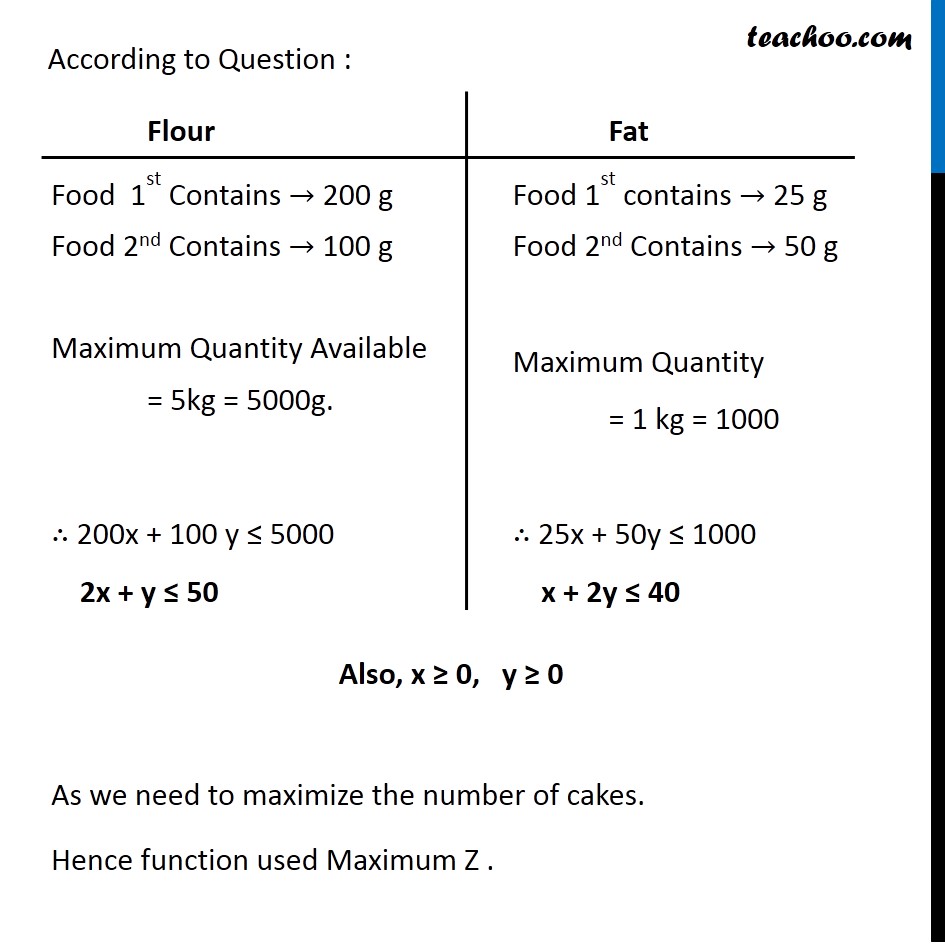
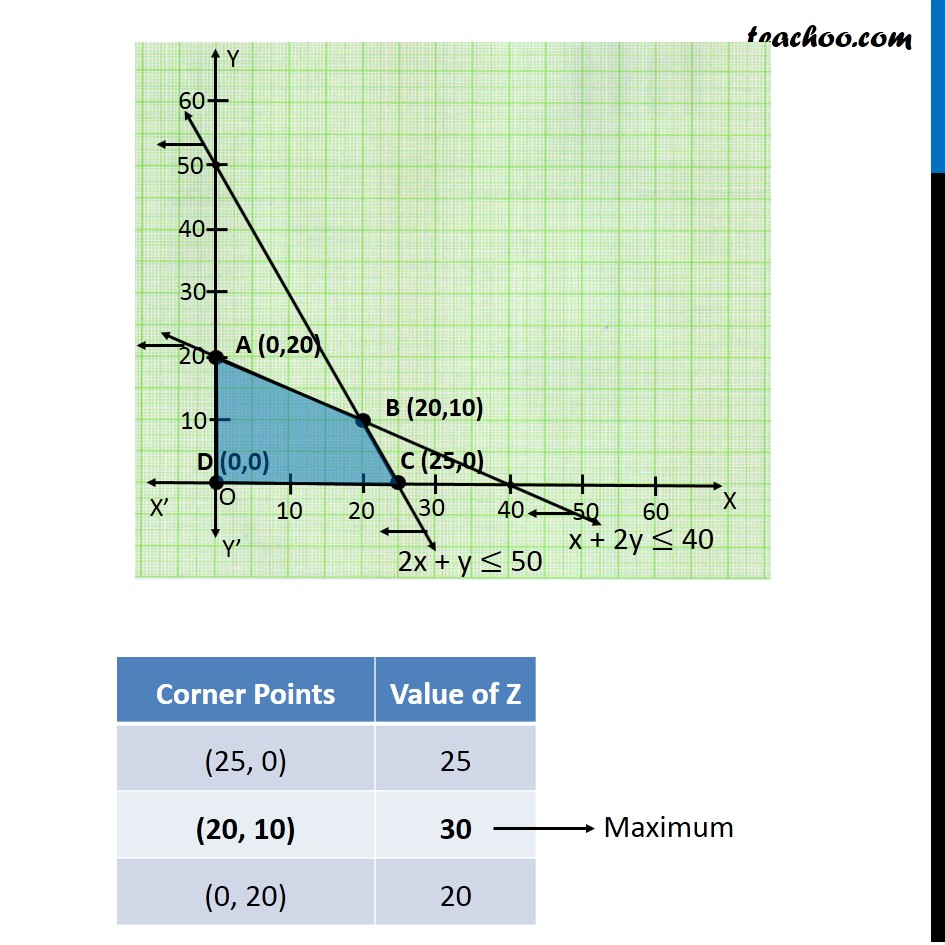
Question 2 One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.Let Number of Cakes of 1st Kind be x and number of cakes of 2nd kind be y. According to Question According to Question : Flour Food 1st Contains → 200 g Food 2nd Contains → 100 g Maximum Quantity Available = 5kg = 5000g. ∴ 200x + 100 y ≤ 5000 2x + y ≤ 50 Fat Food 1st contains → 25 g Food 2nd Contains → 50 g Maximum Quantity = 1 kg = 1000 ∴ 25x + 50y ≤ 1000 x + 2y ≤ 40 Also, x ≥ 0, y ≥ 0 As we need to maximize the number of cakes. Hence function used Maximum Z . Since Total Number of Cakes = x + y Maximize Z = x + y. Combining all constraints Max Z = x + y Subject to constraints : 2x + y ≤ 50 x + 2y ≤ 40 x ≥ 0, y ≥ 0 ∴ Number of cakes will be maximum when Number of cakes of 1st kind are 20 & Number of cakes of 2nd kind are 10. Maximum Number of cakes = 30.