Question 7 - Forming equations and solving - Chapter 12 Class 12 Linear Programming

Transcript

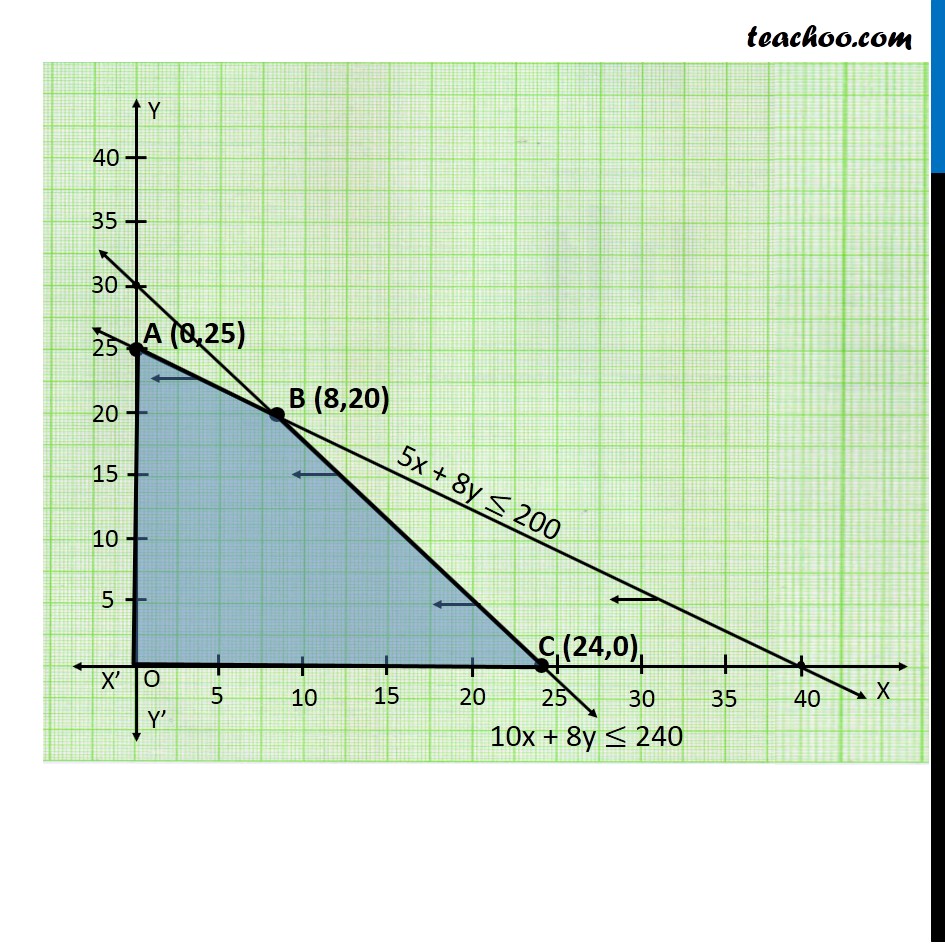
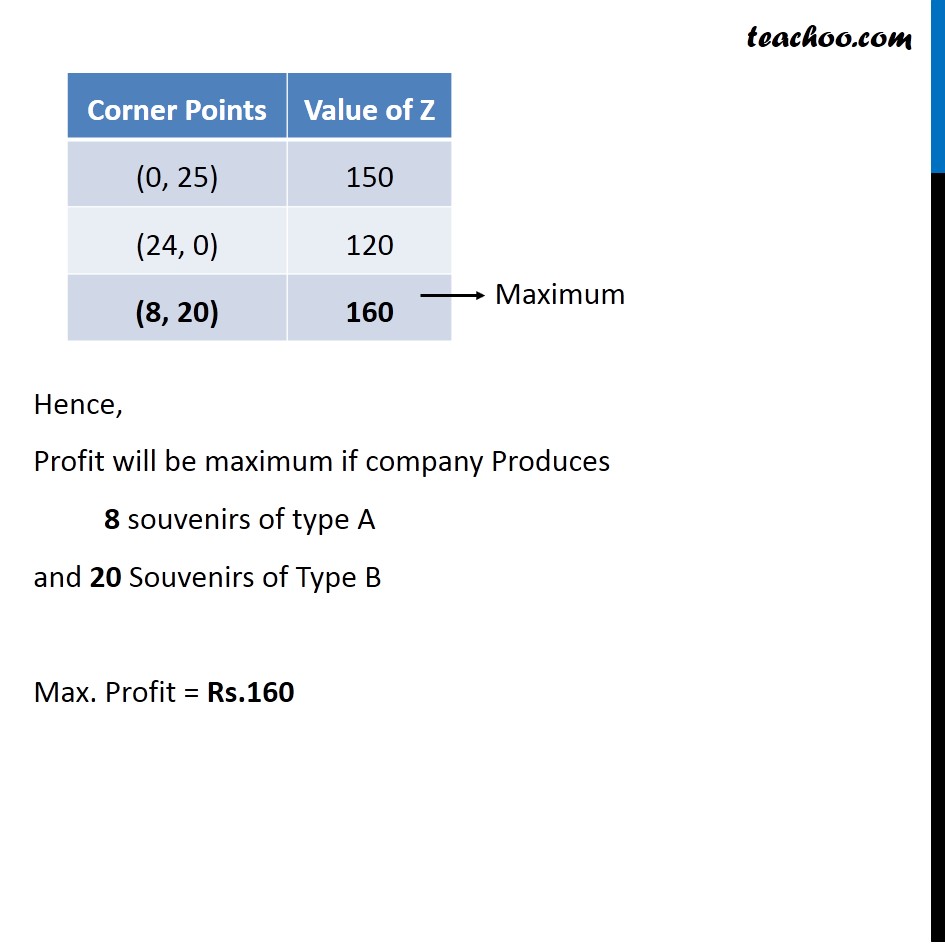
Question 7 A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit?Let the number of souvenirs of type A be x and number of souvenirs of type B be y Cutting Type A requires → 5 min Type B requires → 8 min Maximum Time = 200 min ∴ 5x + 8y ≤ 200 Assembling Type A requires → 10 min Type B requires → 8 min Maximum Time = 240 min ∴ 10x + 8y ≤ 240 As, we need to maximize the profit, so the function used here will be Maximize z. Profit on Type A → Rs. 5 Profit on Type B → Rs. 6∴ Maximize z = 5x + 6y Combining all Constraints : Maximize Z = 5x + 6y Subject to Constraints : 5x + 8y ≤ 200 10x + 8y ≤ 240 x ≥ 0 , y ≥ 0 Hence, Profit will be maximum if company Produces 8 souvenirs of type A and 20 Souvenirs of Type B Max. Profit = Rs.160