Question 1 - Questions easy to difficult - Chapter 9 Class 10 Some Applications of Trigonometry

Transcript

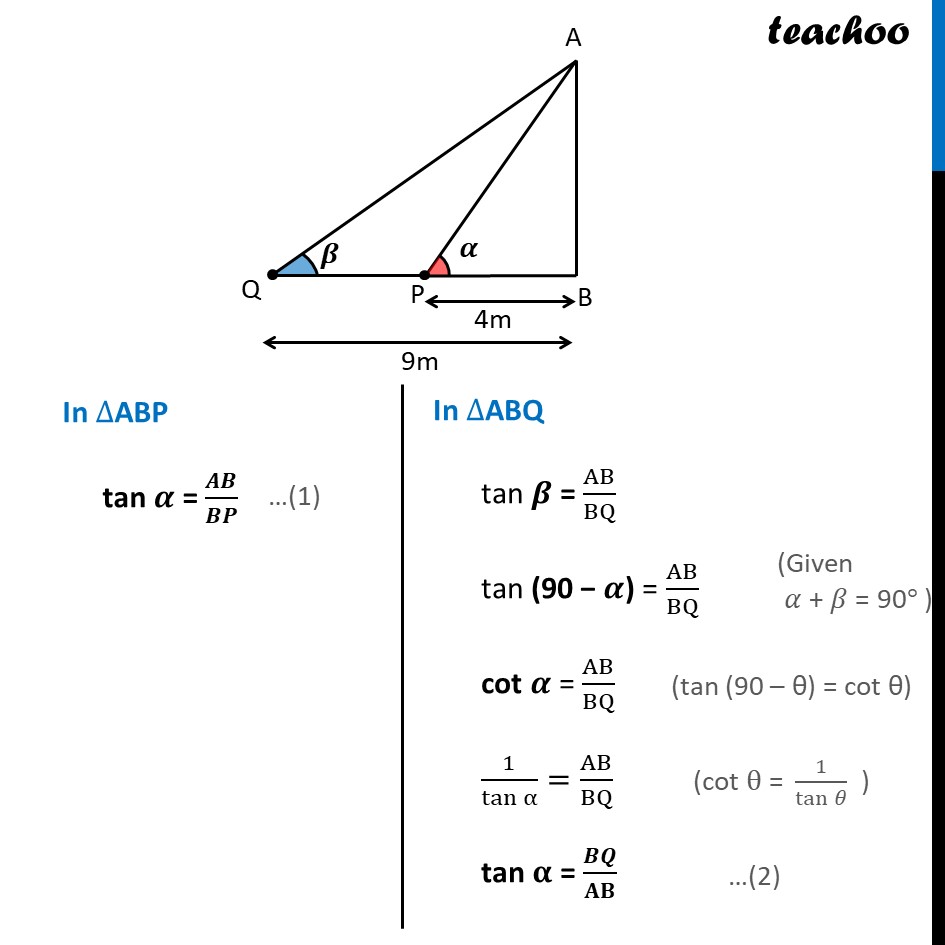
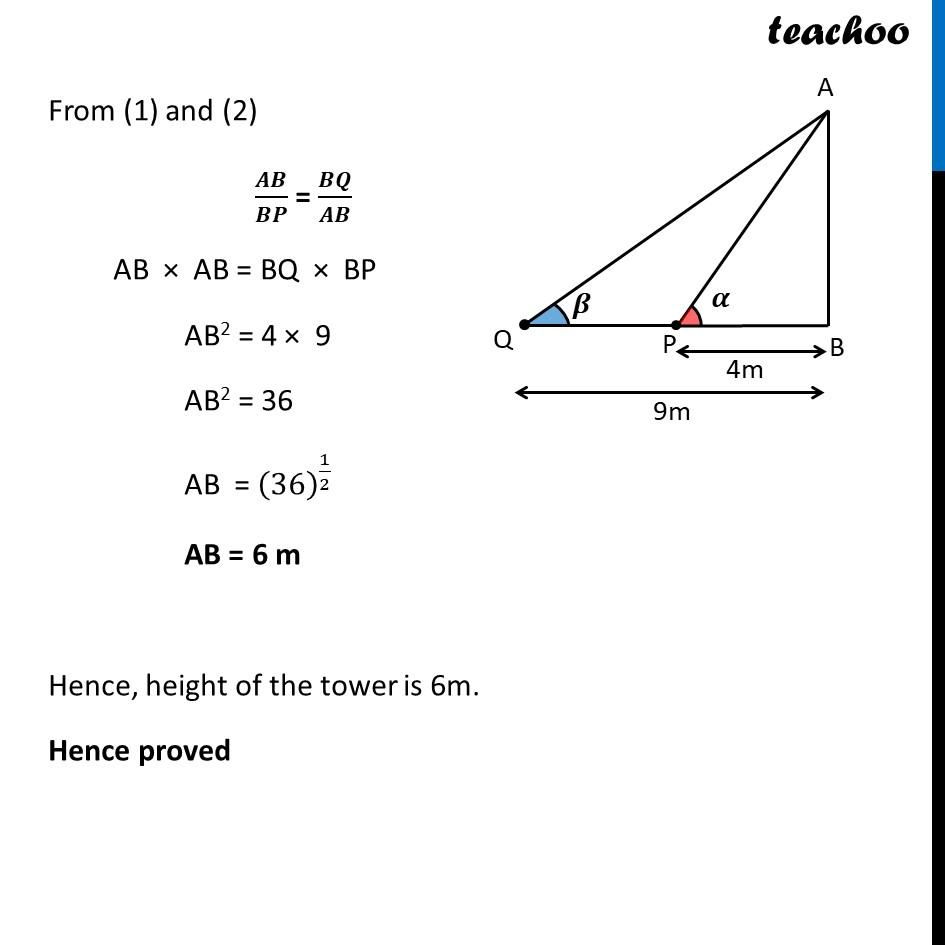
Question 1 The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m. Given that AB is the tower P, Q are the point at distance 4 m and 9 m resp. Also, PB = 4 m , QB = 9 m & Angle of elevation from P is 𝜶 Angle of elevation from Q is 𝜷. Given 𝛼 and 𝛽 are complementary. 𝜶 + 𝜷 = 90° We need to prove AB = 6 m In ∆ABP tan 𝜶 = 𝑨𝑩/𝑩𝑷 In ∆ABQ tan 𝜷 = AB/BQ tan (90 − 𝜶) = AB/BQ cot 𝜶 = AB/BQ 1/(tan α)=AB/BQ tan 𝛂 = 𝑩𝑸/𝐀𝐁 From (1) and (2) 𝑨𝑩/𝑩𝑷 = 𝑩𝑸/𝑨𝑩 AB × AB = BQ × BP AB2 = 4 × 9 AB2 = 36 AB = (36)^(1/2) AB = 6 m Hence, height of the tower is 6m. Hence proved