Ex 9.1, 12 - Chapter 9 Class 10 Some Applications of Trigonometry

Transcript

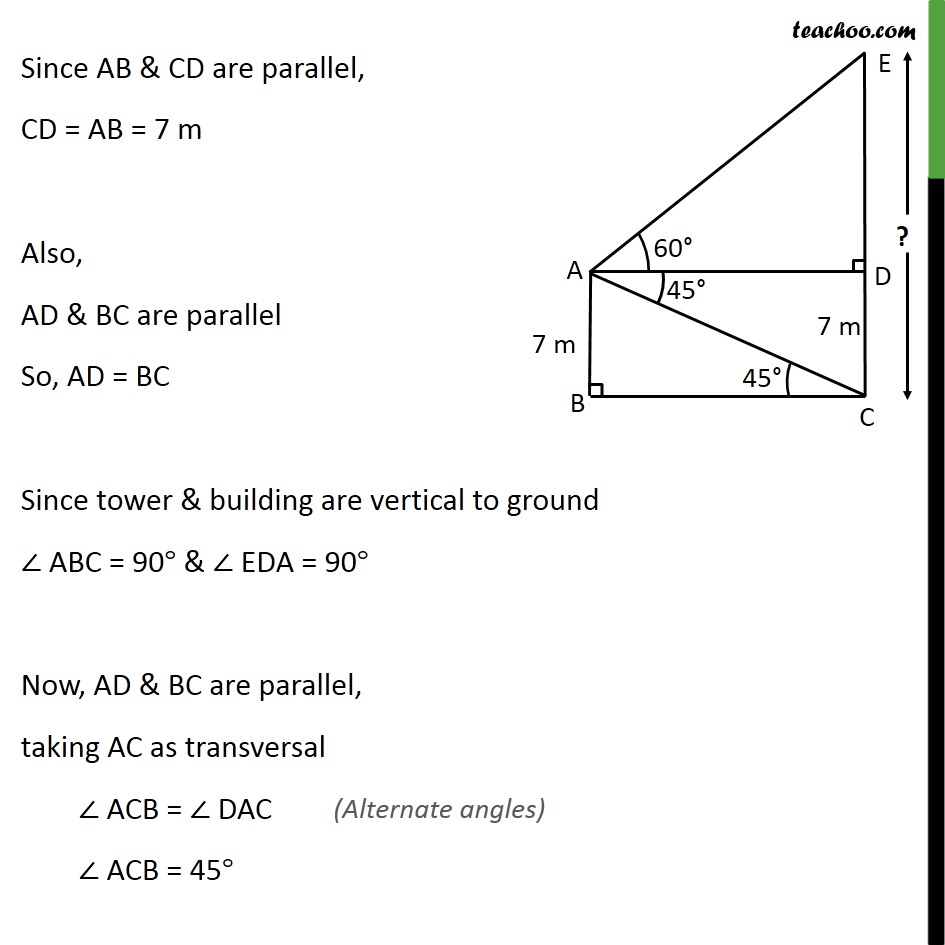
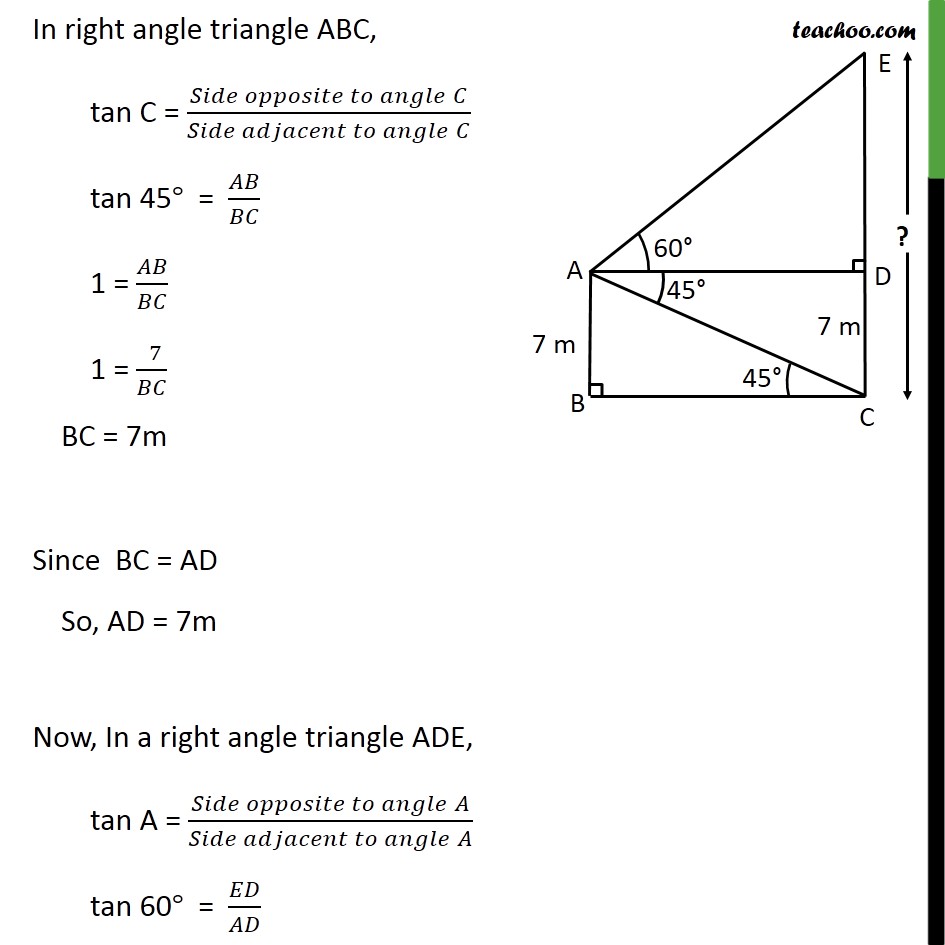
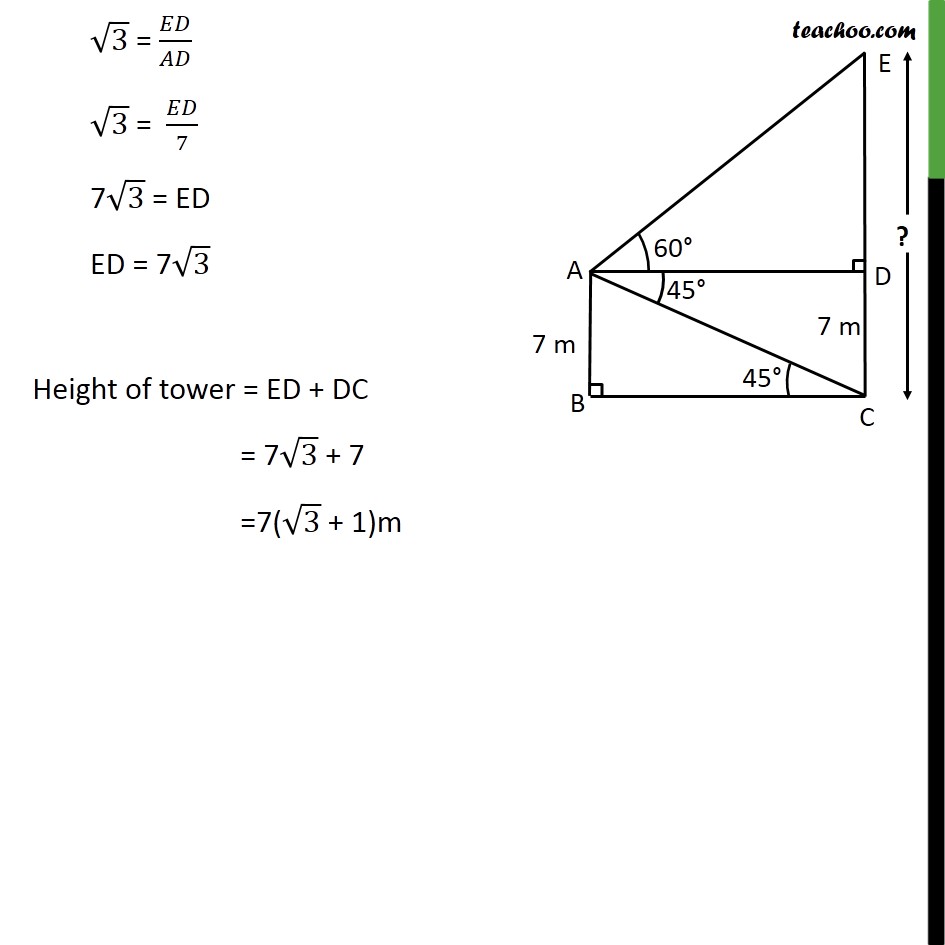
Ex 9.1 , 12 From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. Let building be AB & tower be CE Given height of building = AB = 7m From the top of building, angle of elevation of top of tower = 60°. Hence, ∠EAD = 60° Angle of depression of the foot of the tower = 45° Hence, ∠CAD = 45° We need to find height of tower i.e. CE Since AB & CD are parallel, CD = AB = 7 m Also, AD & BC are parallel So, AD = BC Since tower & building are vertical to ground ∠ ABC = 90° & ∠ EDA = 90° Now, AD & BC are parallel, taking AC as transversal ∠ ACB = ∠ DAC ∠ ACB = 45° In right angle triangle ABC, tan C = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐶)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐶) tan 45° = 𝐴𝐵/𝐵𝐶 1 = 𝐴𝐵/𝐵𝐶 1 = (" " 7)/𝐵𝐶 BC = 7m Since BC = AD So, AD = 7m Now, In a right angle triangle ADE, tan A = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐴)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐴) tan 60° = 𝐸𝐷/𝐴𝐷 √3 = 𝐸𝐷/𝐴𝐷 √3 = 𝐸𝐷/7 7√3 = ED ED = 7√3 Height of tower = ED + DC = 7√3 + 7 =7(√3 + 1)m