
Questions easy to difficult
Last updated at Dec. 13, 2024 by Teachoo


Transcript
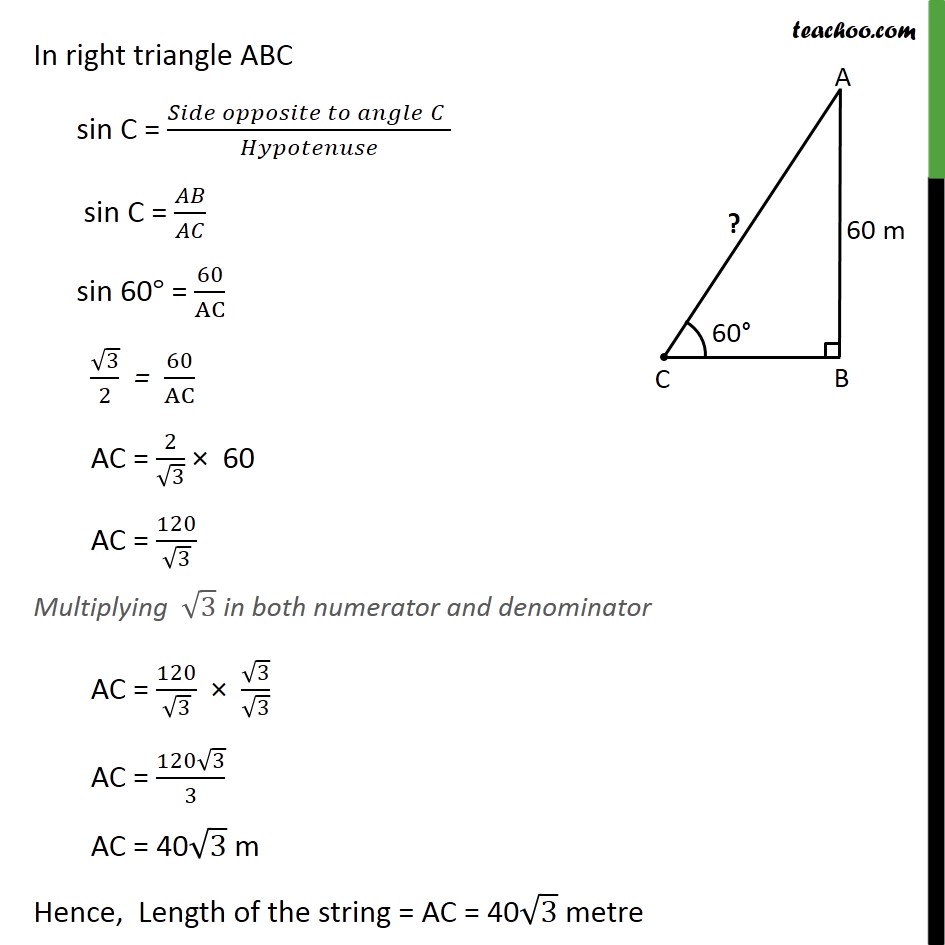
Ex 9.1 , 5 A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string. Given that, Height at which kite is flying = 60 metre Hence, AB = 60 m Also, inclination of the string with the ground = 60° Hence, ∠ACB = 60° We have to find length of string, i.e., AC Here, AB is perpendicular to ground So, ∠ ABC = 90° In right triangle ABC sin C = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐶" " )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 sin C = 𝐴𝐵/𝐴𝐶 sin 60° = 60/AC √3/2 = 60/AC AC = 2/√3 × 60 AC = 120/√3 Multiplying √3 in both numerator and denominator AC = 120/√3 × √3/√3 AC = (120√3)/3 AC = 40√3 m Hence, Length of the string = AC = 40√3 metre