Example 6 - Chapter 9 Class 10 Some Applications of Trigonometry

Transcript

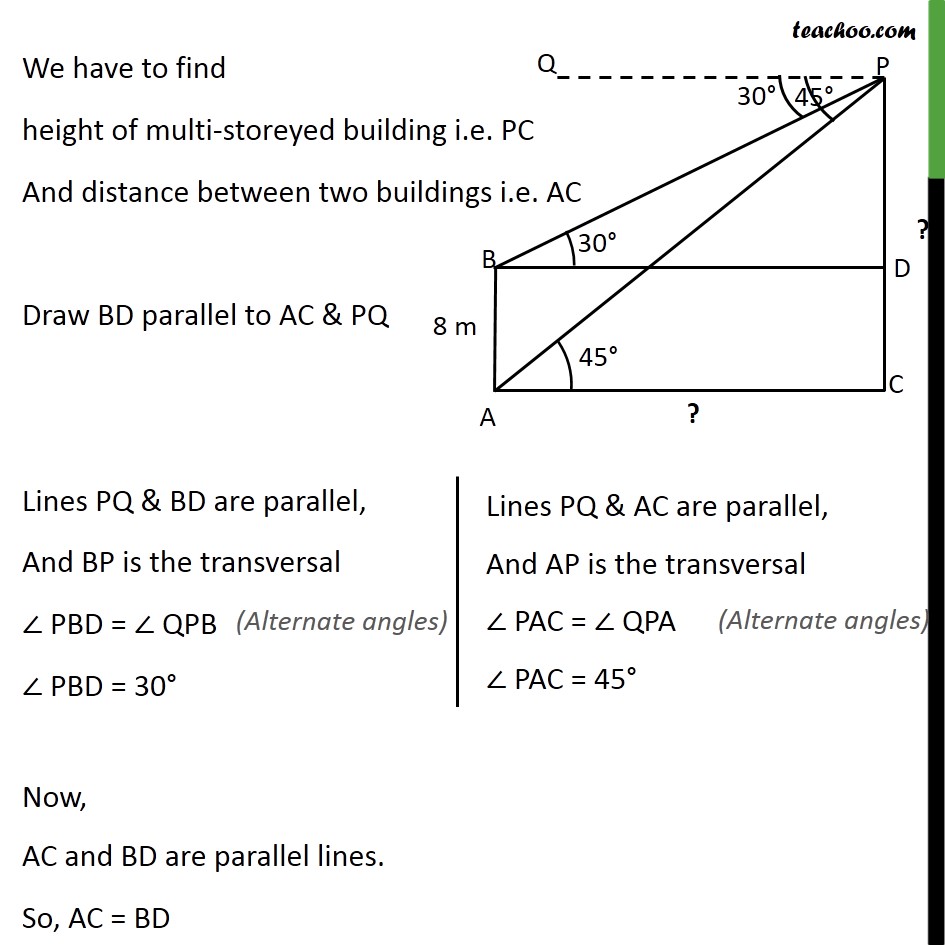
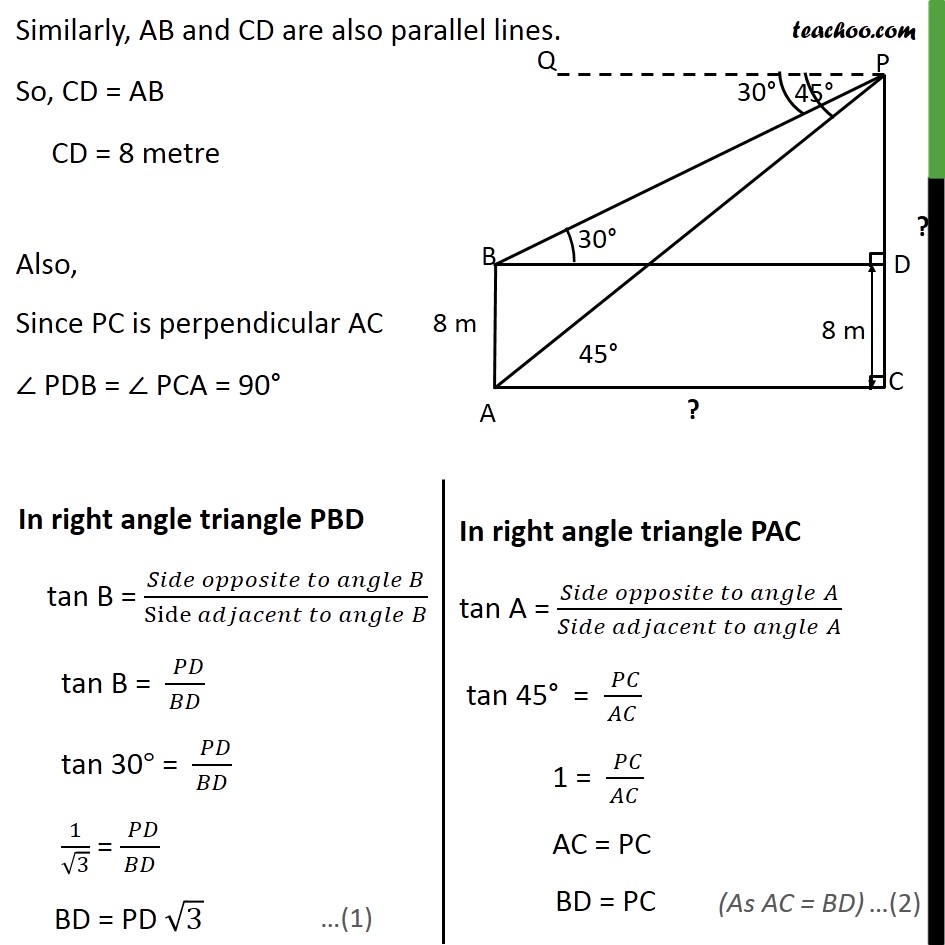
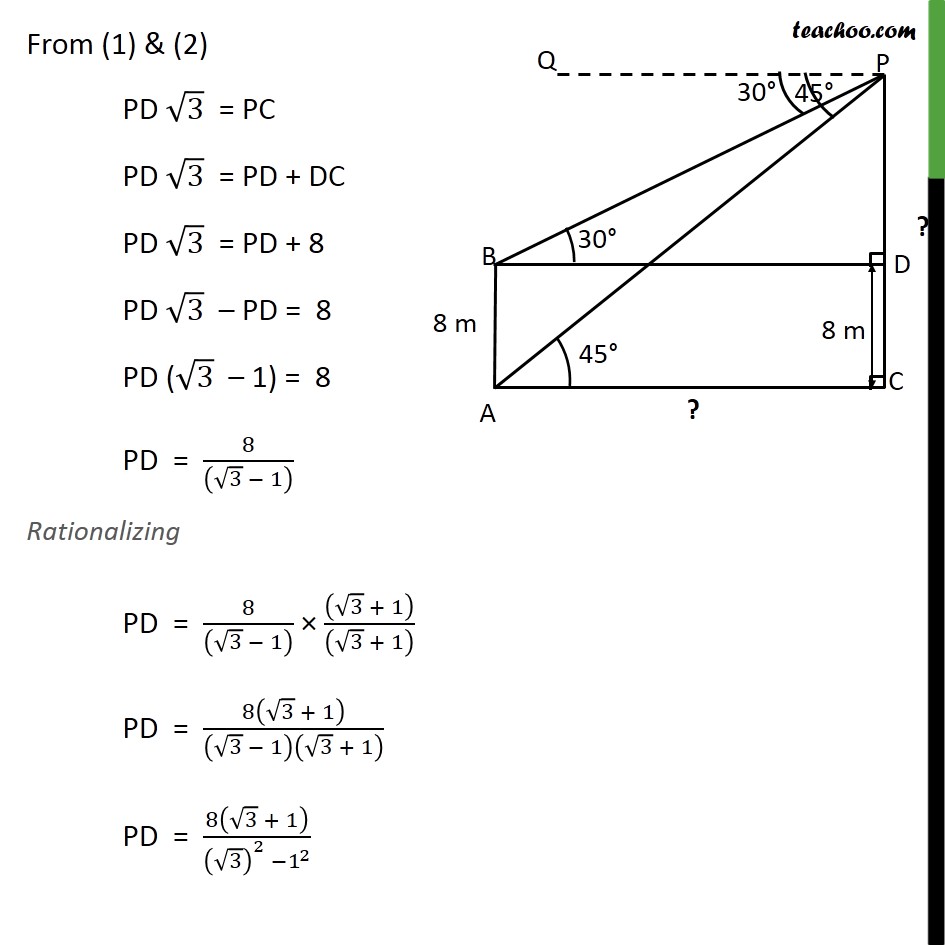
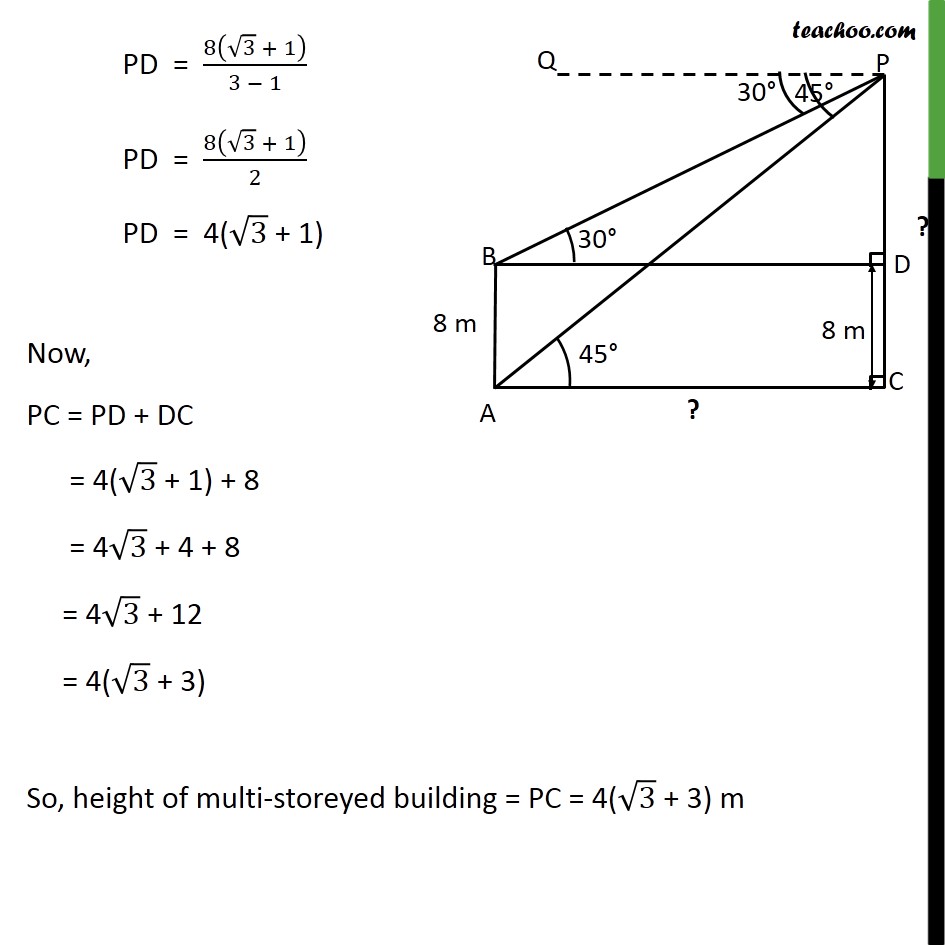
Example 6 The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30 and 45 , respectively. Find the height of the multi-storeyed building and the distance between the two buildings. Height of tall building (AB) = 8m Let, Height of the multi-storeyed building = PC And, distance between two building = AC Angle of depression to top of building = QPB = 30 Angle of depression to bottom of building = QPA = 45 We have to find height of multi-storeyed building i.e. PC And distance between two buildings i.e. AC Draw BD parallel to AC & PQ Lines PQ & BD are parallel, And BP is the transversal PBD = QPB PBD = 30 Now, AC and BD are parallel lines. So, AC = BD Similarly, AB and CD are also parallel lines. So, CD = AB CD = 8 metre Also, Since PC is perpendicular AC PDB = PCA = 90 From (1) & (2) PD 3 = PC PD 3 = PD + DC PD 3 = PD + 8 PD 3 PD = 8 PD ( 3 1) = 8 PD = 8/(( 3 1) ) Rationalizing PD = 8/(( 3 1) ) (( 3 + 1))/(( 3 + 1) ) PD = 8( 3 + 1)/( 3 1)( 3 + 1) PD = 8( 3 + 1)/(( 3)^2 1^2 ) PD = 8( 3 + 1)/(3 1) PD = 8( 3 + 1)/2 PD = 4( 3 + 1) Now, PC = PD + DC = 4( 3 + 1) + 8 = 4 3 + 4 + 8 = 4 3 + 12 = 4( 3 + 3) So, height of multi-storeyed building = PC = 4( 3 + 3) m From (1) BD = PD 3 BD = 4( 3 + 1) 3 BD = 4 3 ( 3 + 1) BD = 4 3 " " 3 + 4 3 " " 1 BD = 4(3) + 4 3 BD = 12 + 4 3 BD = 4(3 + 3) m So, AC = BD = 4(3 + 3) m Distance between two buildings = AC = 4(3 + 3) m