Misc 5 (MCQ) - Chapter 8 Class 12 Application of Integrals

Transcript

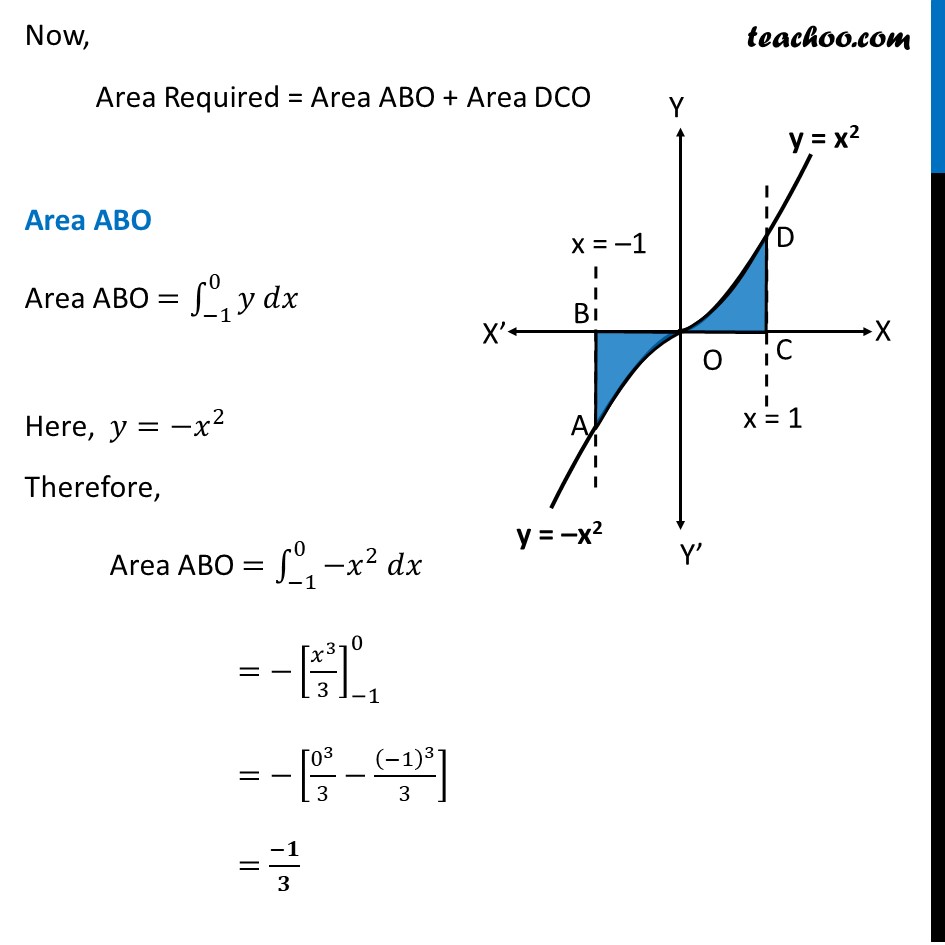
Misc 5 The area bounded by the curve 𝑦 = 𝑥 |𝑥| , 𝑥−𝑎𝑥𝑖𝑠 and the ordinates 𝑥 = – 1 and 𝑥=1 is given by (A) 0 (B) 1/3 (C) 2/3 (D) 4/3 [Hint : 𝑦=𝑥2 if 𝑥 > 0 𝑎𝑛𝑑 𝑦 =−𝑥2 if 𝑥 < 0]We know that |𝑥|={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ Therefore, y = x|𝒙|={█(𝒙𝒙, 𝒙≥𝟎@&𝒙(−𝒙), 𝒙<𝟎)┤ y ={█(𝑥^2, 𝑥≥0@&−𝑥^2, 𝑥<0)┤ Now, Area Required = Area ABO + Area DCO Area ABO Area ABO =∫_(−1)^0▒〖𝑦 𝑑𝑥〗 Here, 𝑦=〖−𝑥〗^2 Therefore, Area ABO =∫_(−1)^0▒〖〖−𝑥〗^2 𝑑𝑥〗 〖=−[𝑥^3/3]〗_(−1)^0 =−[0^3/3−(−1)^3/3] =(−𝟏)/𝟑 Since Area is always positive, Area ABO = 𝟏/𝟑 Area DCO Area DCO =∫_0^1▒〖𝑦 𝑑𝑥〗 Here, 𝑦=𝑥^2 Therefore, Area DCO =∫_𝟎^𝟏▒〖𝒙^𝟐 𝒅𝒙〗 〖=[𝑥^3/3]〗_0^1 =1/3 [1^3−0^3 ] =1/3 [1−0] =𝟏/𝟑 Therefore, Required Area = Area ABO + Area DCO =1/3+1/3 =𝟐/𝟑 square units So, the correct answer is (c)