Question 6 - Area bounded by curve and horizontal or vertical line - Chapter 8 Class 12 Application of Integrals

Transcript

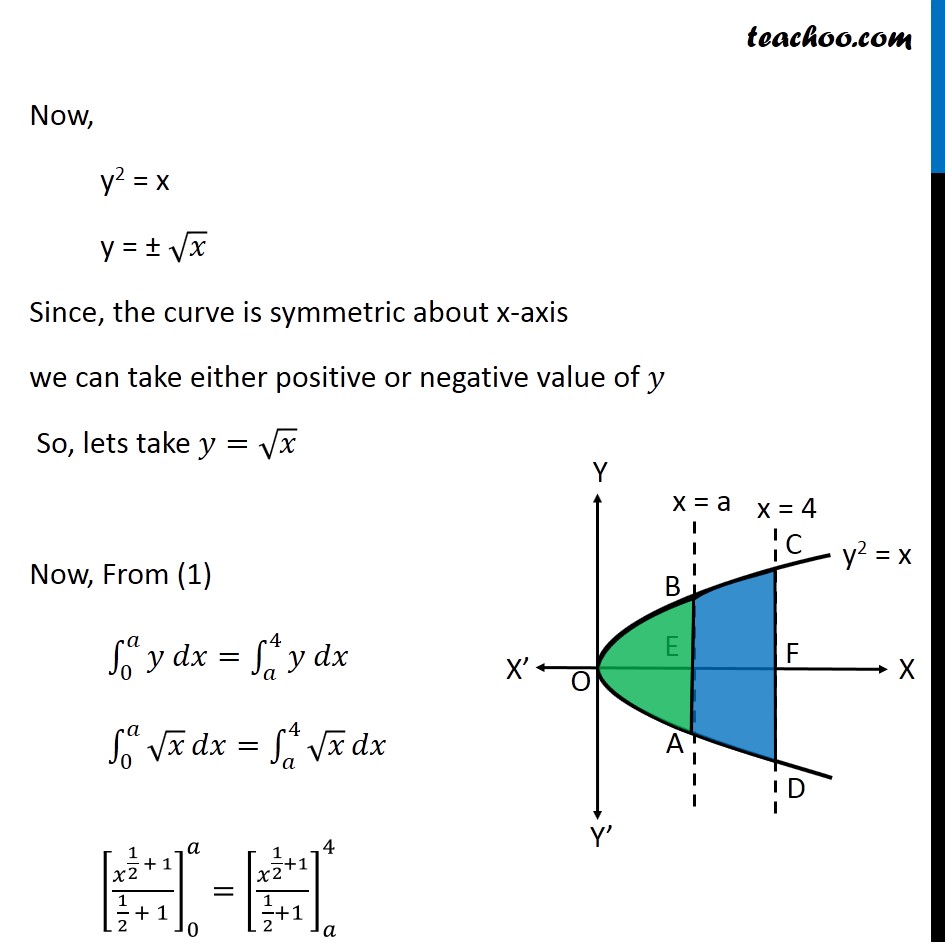
Question 6 The area between 𝑥=𝑦2 and 𝑥 = 4 is divided into two equal parts by the line 𝑥=𝑎, find the value of a. Given curve 𝑦^2=𝑥 Let AB represent the line 𝑥=𝑎 CD represent the line 𝑥=4 Since the line 𝑥=𝑎 divides the region into two equal parts ∴ Area of OBA = Area of ABCD 2 × ∫_0^𝑎▒〖𝑦 𝑑𝑥〗="2 ×" ∫_𝑎^4▒〖𝑦 𝑑𝑥〗 ∫_𝟎^𝒂▒〖𝒚 𝒅𝒙〗=∫_𝒂^𝟒▒〖𝒚 𝒅𝒙〗 Now, y2 = x y = ± √𝑥 Since, the curve is symmetric about x-axis we can take either positive or negative value of 𝑦 So, lets take 𝑦=√𝑥 Now, From (1) ∫_0^𝑎▒〖𝑦 𝑑𝑥〗=∫_𝑎^4▒〖𝑦 𝑑𝑥〗 ∫_0^𝑎▒√𝑥 𝑑𝑥=∫_𝑎^4▒√𝑥 𝑑𝑥 [𝑥^(1/2 + 1)/(1/2 + 1)]_0^𝑎=[𝑥^(1/2+1)/(1/2+1)]_𝑎^4 [𝑥^((1+2)/2) ]_0^𝑎=[𝑥^((1+2)/2) ]_𝑎^4 [𝑥^(3/2) ]_0^𝑎=[𝑥^(3/2) ]_𝑎^4 (𝑎)^(3/2)−0=(4)^(3/2)−(𝑎)^(3/2) 2(𝑎)^(3/2)=(4)^(3/2) Taking 〖2/3〗^𝑡ℎ root on both sides (2)^(2/3) 𝑎^(3/2 × 2/3)=4^(3/2 × 2/3) (2)^(2/3) 𝑎=4 𝑎=(2)^2/(2)^(2/3) 𝑎=(2)^(2 − 2/3) 𝑎=(2)^((6 − 2)/3) 𝑎=(2)^(4/3) 𝑎=(2)^(2 × 2/3) 𝑎=[2^2 ]^(2/3) 𝒂=(𝟒)^(𝟐/𝟑) So, value of a is (4)^(2/3)