Question 3 - Area bounded by curve and horizontal or vertical line - Chapter 8 Class 12 Application of Integrals

Transcript

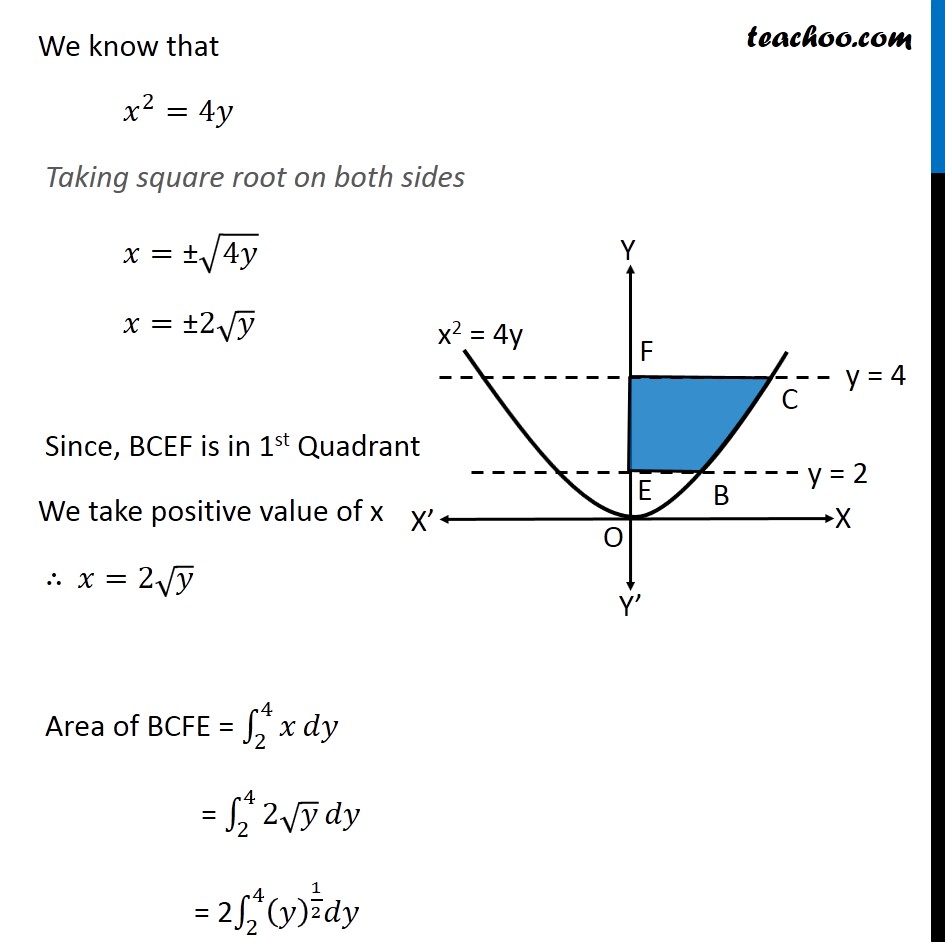
Question 3 Find the area of the region bounded by 𝑥2= 4𝑦 , 𝑦 = 2 , 𝑦=4 and the 𝑦-axis in the first quadrant. Here, The curve is 𝑥^2=4𝑦 We have to find area between y = 2 and y = 4 ∴ We have to find area of BCFE Area of BCFE = ∫_2^4▒𝑥 𝑑𝑦 We know that 𝑥^2=4𝑦 Taking square root on both sides 𝑥="±" √4𝑦‖ 𝑥="±" 2√𝑦 Since, BCEF is in 1st Quadrant We take positive value of x ∴ 𝑥=2√𝑦 Area of BCFE = ∫_2^4▒𝑥 𝑑𝑦 = ∫_2^4▒〖2√𝑦〗 𝑑𝑦 = 2∫_2^4▒〖(𝑦)^(1/2) 𝑑𝑦〗 = 2 [𝑦^(3/2)/(3/2)]_2^4 = 2 × 2/3 [𝑦^(3/2) ]_2^4 = 4/3 [(4)^(3/2 )−(2)^(3/2) ] = 4/3 [((4)^(1/2) )^3−((2)^(1/2) )^3 ] = 4/3 [(2)^3−(√2)^3 ] = 4/3 [8 −2√2] = (32 − 8√2)/3 Thus, Area = (𝟑𝟐 − 𝟖√𝟐)/𝟑 square units