Misc 2 - Chapter 8 Class 12 Application of Integrals

Transcript

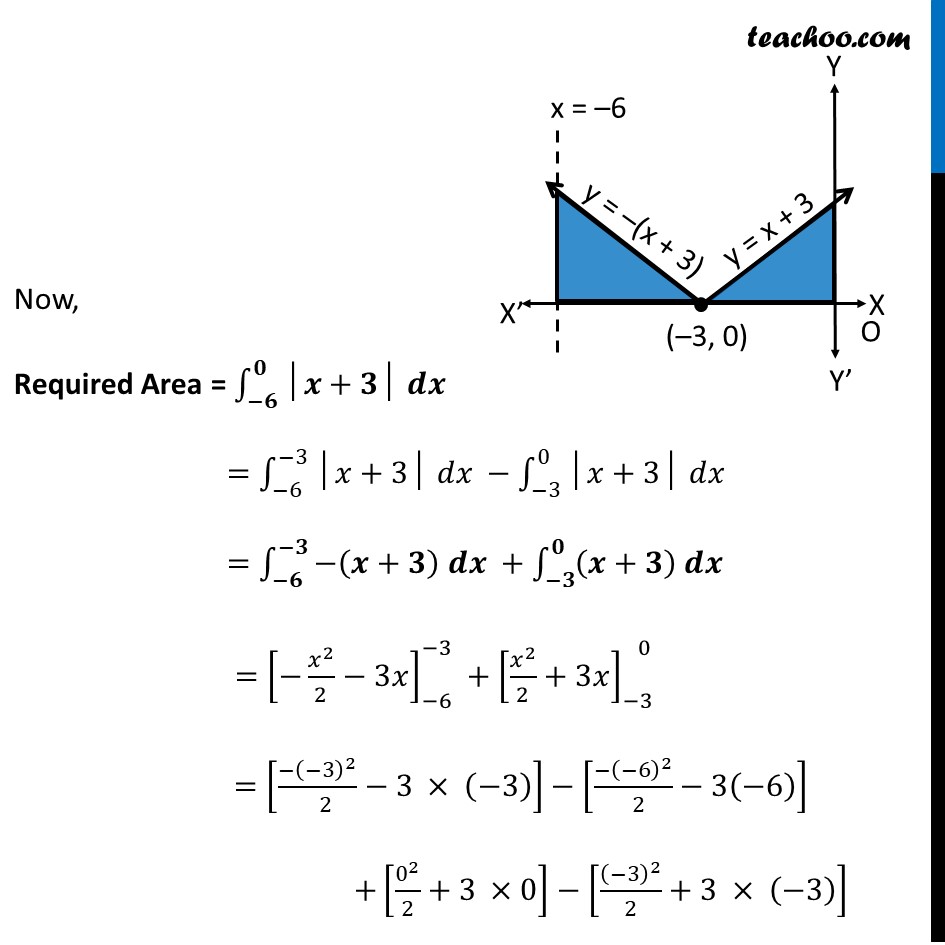
Misc 2 Sketch the graph of y = |𝑥+3| and evaluate ∫_(−6)^0▒〖│𝑥+3│ 𝑑𝑥〗 Let’s Draw the graph y = |𝒙+𝟑| y = |𝑥+3| = {█(𝑥+3 𝑓𝑜𝑟 𝑥+3≥0@−(𝑥+3) 𝑓𝑜𝑟 𝑥+3<0 )┤ = {█(𝑥+3 𝑓𝑜𝑟 𝑥≥−3@−(𝑥+3) 𝑓𝑜𝑟 𝑥+3<−3 )┤ Now, Required Area = ∫_(−𝟔)^𝟎▒〖│𝒙+𝟑│ 𝒅𝒙〗 =∫_(−6)^(−3)▒〖│𝑥+3│ 𝑑𝑥〗 −∫_(−3)^0▒〖│𝑥+3│ 𝑑𝑥〗 =∫_(−𝟔)^(−𝟑)▒〖−(𝒙+𝟑) 𝒅𝒙 +∫_(−𝟑)^𝟎▒〖(𝒙+𝟑) 𝒅𝒙〗〗 =[−𝑥^2/2−3𝑥]_(−6)^(−3) +[𝑥^2/2+3𝑥]_(−3)^( 0) =[(−(−3)^2)/( 2)−3 × (−3)]−[(−(−6)^2)/( 2)−3(−6)] +[0^2/2+3 ×0]−[(−3)^2/2+3 × (−3)] =[(−9)/( 2)−(−9)]−[(−36)/( 2)−(−18)]+[0]−[9/2−9] =(−9)/2+9+0−9/2+9 =−9+18 =𝟗 square units