Question 4 - Area between curve and curve - Chapter 8 Class 12 Application of Integrals

Transcript

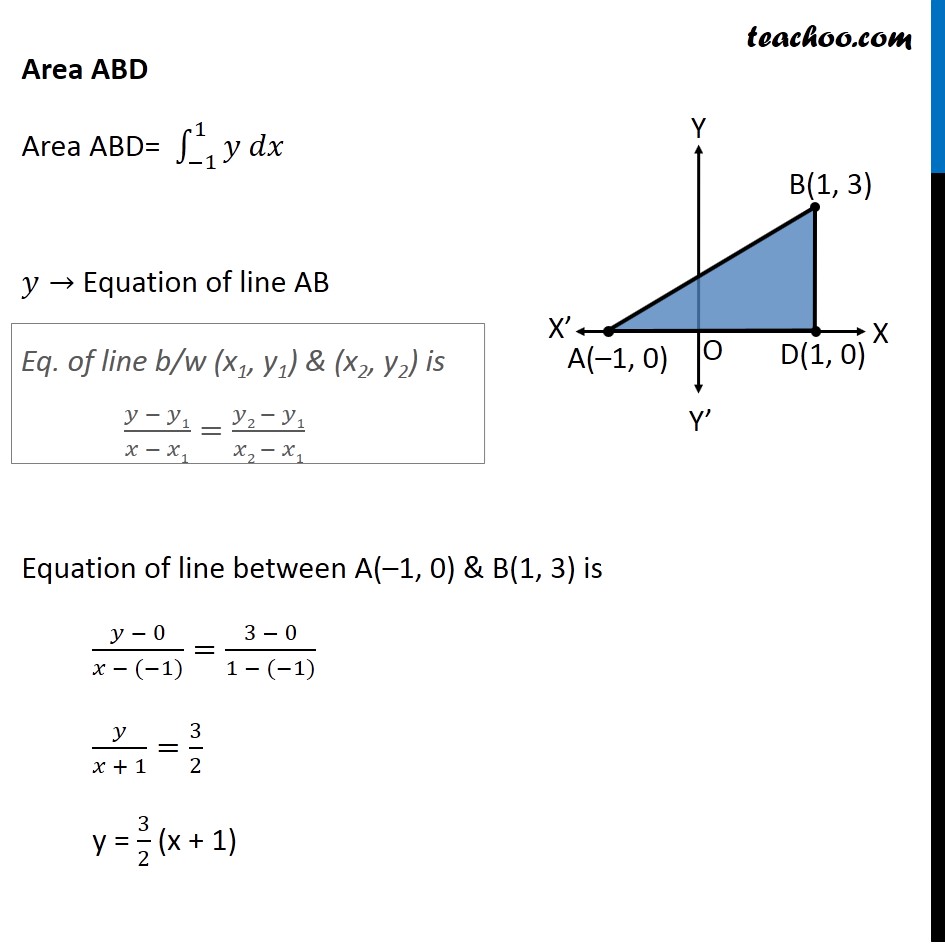
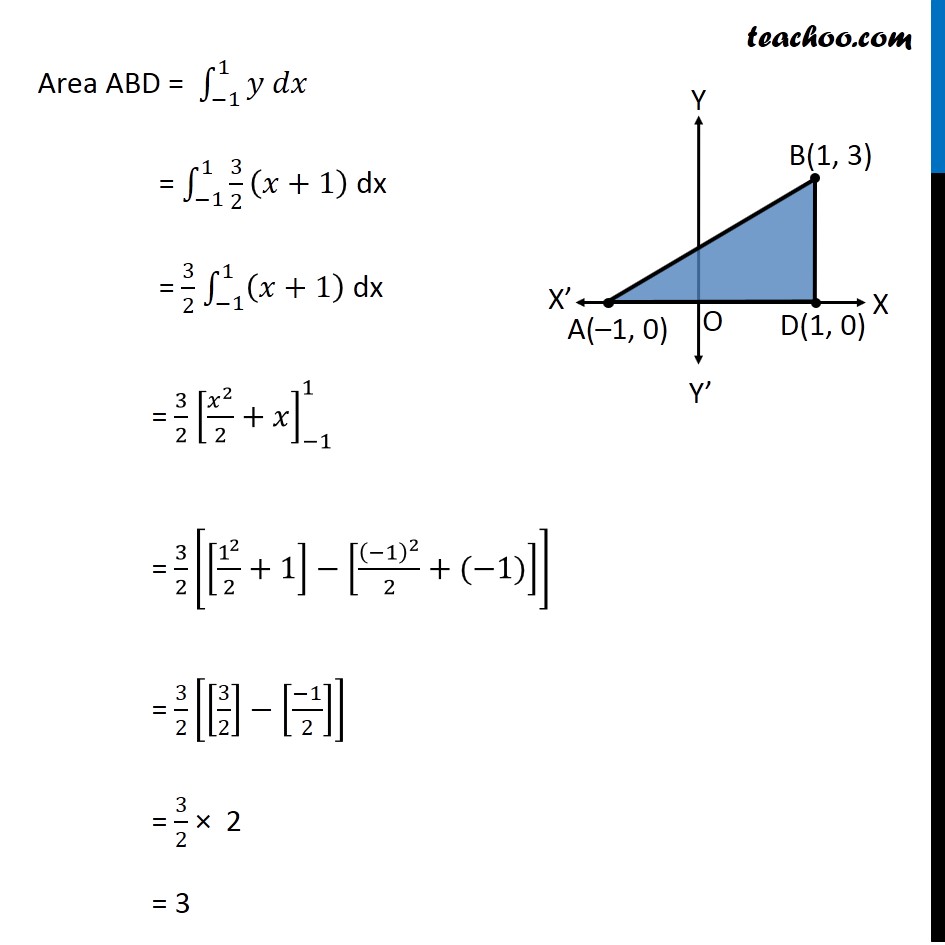
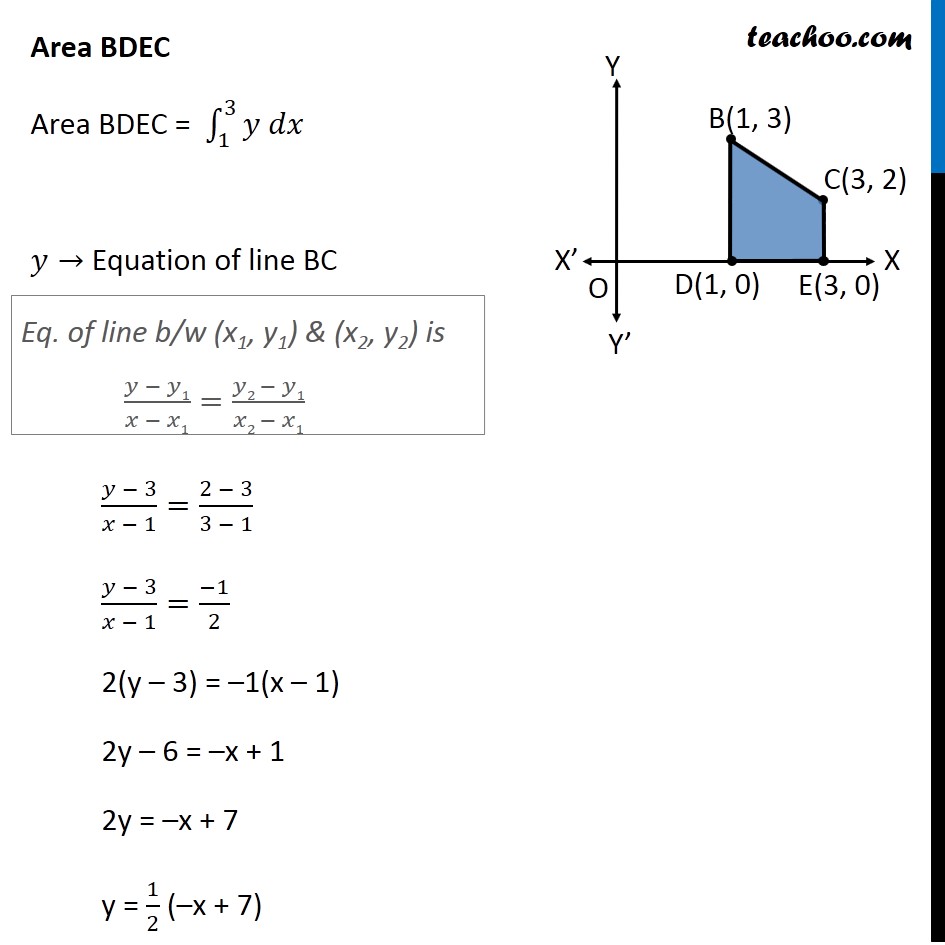
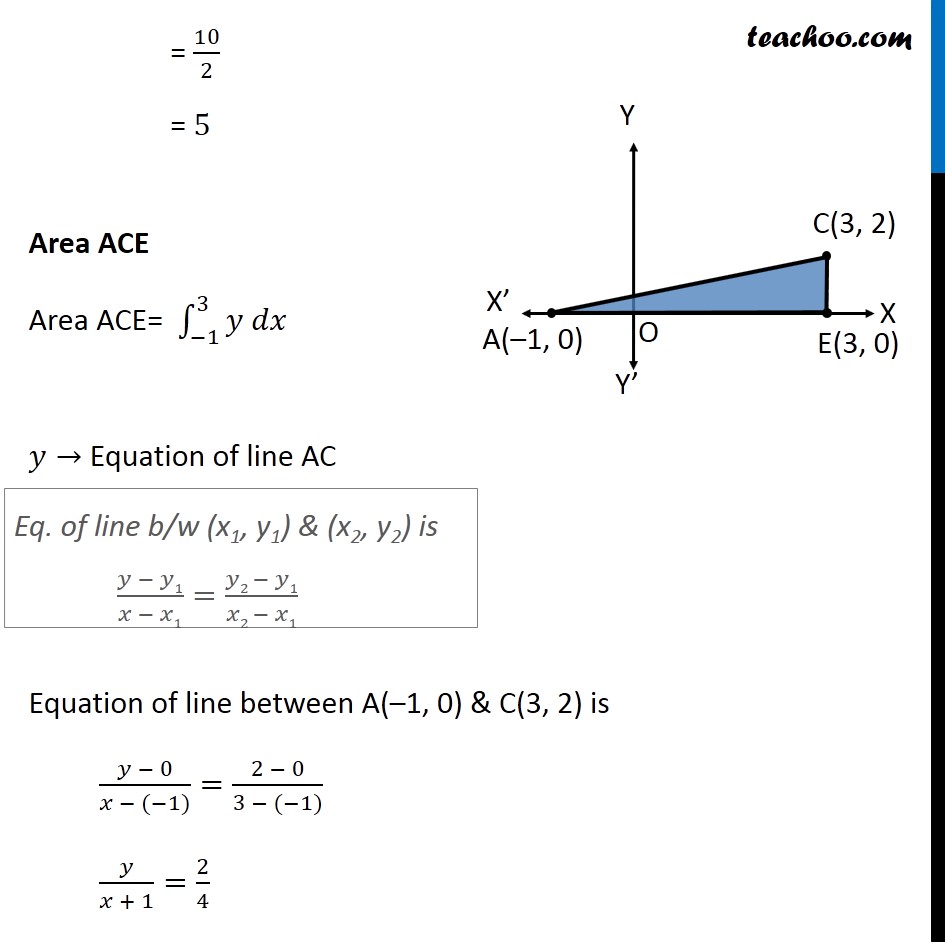
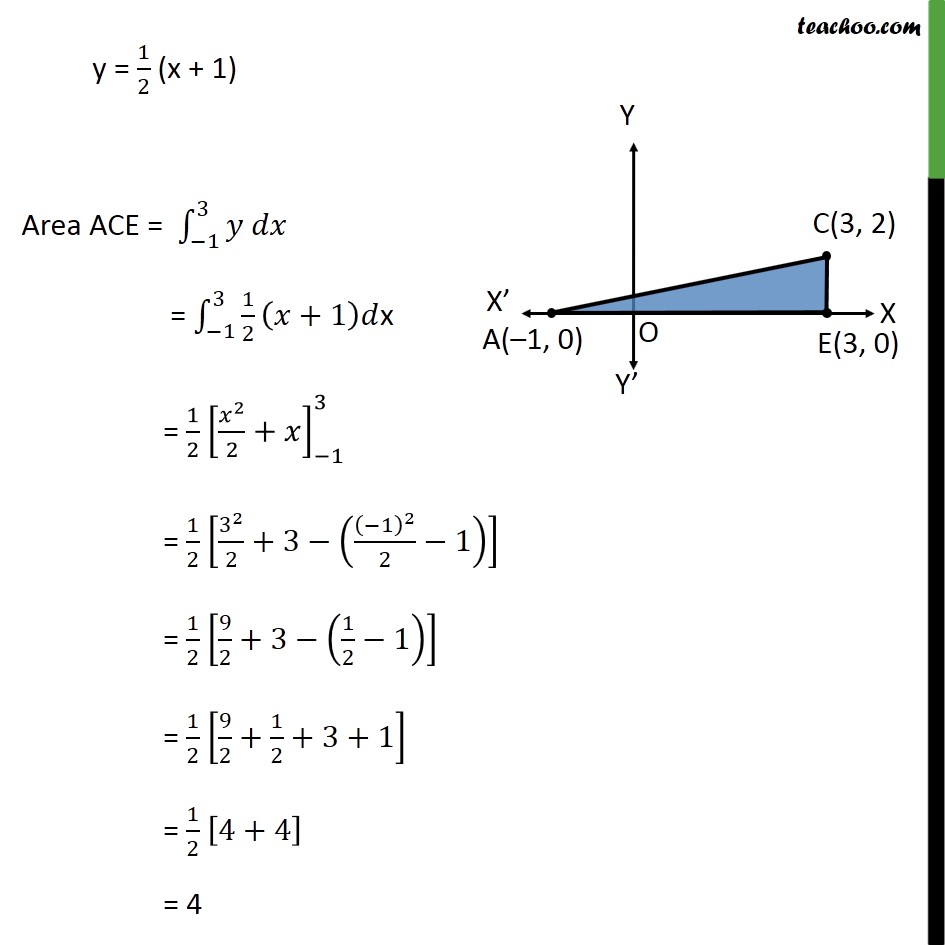
Question 4 Using integration find the area of region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2) Let points be A(– 1, 0), B(1, 3) and C(3, 2) We mark the points on the diagram Area Δ ABC = Area ABD + Area BDEC – Area ACE Area ABD Area ABD= ∫_(−1)^1▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of line AB Equation of line between A(–1, 0) & B(1, 3) is (𝑦 − 0)/(𝑥 − (−1))=(3 − 0)/(1 − (−1)) 𝑦/(𝑥 + 1)=3/2 y = 3/2 (x + 1) Eq. of line b/w (x1, y1) & (x2, y2) is (𝑦 − 𝑦1)/(𝑥 − 𝑥1)=(𝑦2 − 𝑦1)/(𝑥2 − 𝑥1) Area ABD = ∫_(−1)^1▒〖𝑦 𝑑𝑥〗 = ∫1_(−1)^1▒〖3/2 (𝑥+1) 〗 dx = 3/2 ∫1_(−1)^1▒(𝑥+1) dx = 3/2 [𝑥^2/2+𝑥]_(−1)^1 = 3/2 [[1^2/2+1]−[(−1)^2/2+(−1)]] = 3/2 [[3/2]−[(−1)/2]] = 3/2 × 2 = 3 Area BDEC Area BDEC = ∫_1^3▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of line BC (𝑦 − 3)/(𝑥 − 1)=(2 − 3)/(3 − 1) (𝑦 − 3)/(𝑥 − 1)=(−1)/2 2(y – 3) = –1(x – 1) 2y – 6 = –x + 1 2y = –x + 7 y = 1/2 (–x + 7) Eq. of line b/w (x1, y1) & (x2, y2) is (𝑦 − 𝑦1)/(𝑥 − 𝑥1)=(𝑦2 − 𝑦1)/(𝑥2 − 𝑥1) Area BDEC = ∫_1^3▒〖𝑦 𝑑𝑥〗 = ∫1_1^3▒〖1/2 (−𝑥+7)𝑑〗x = 1/2 [〖−𝑥〗^2/2+7𝑥]_1^3 = 1/2 [[〖−3〗^2/2+7(3)]− [〖(−1)/2〗^2+7(1)]] = 1/2 [(−9)/2+21+1/2−7] = 1/2 [(−9 + 1)/2+14] = 1/2 [(−8)/2+14] = 1/2 [−4+14] = 10/2 = 5 Area ACE Area ACE= ∫_(−1)^3▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of line AC Equation of line between A(–1, 0) & C(3, 2) is (𝑦 − 0)/(𝑥 − (−1))=(2 − 0)/(3 − (−1)) 𝑦/(𝑥 + 1)=2/4 Eq. of line b/w (x1, y1) & (x2, y2) is (𝑦 − 𝑦1)/(𝑥 − 𝑥1)=(𝑦2 − 𝑦1)/(𝑥2 − 𝑥1) y = 1/2 (x + 1) Area ACE = ∫_(−1)^3▒〖𝑦 𝑑𝑥〗 = ∫1_(−1)^3▒〖1/2 (𝑥+1)𝑑〗x = 1/2 [𝑥^2/2+𝑥]_(−1)^3 = 1/2 [3^2/2+3−((−1)^2/2−1)] = 1/2 [9/2+3−(1/2−1)] = 1/2 [9/2+1/2+3+1] = 1/2 [4+4] = 4 Hence, Required area = Area ABD + Area BDEC − Area ACE = 3 + 5 − 4 = 4 square units