Question 10 - Using Property 5 (Determinant as sum of two or more determinants) - Chapter 4 Class 12 Determinants

Transcript

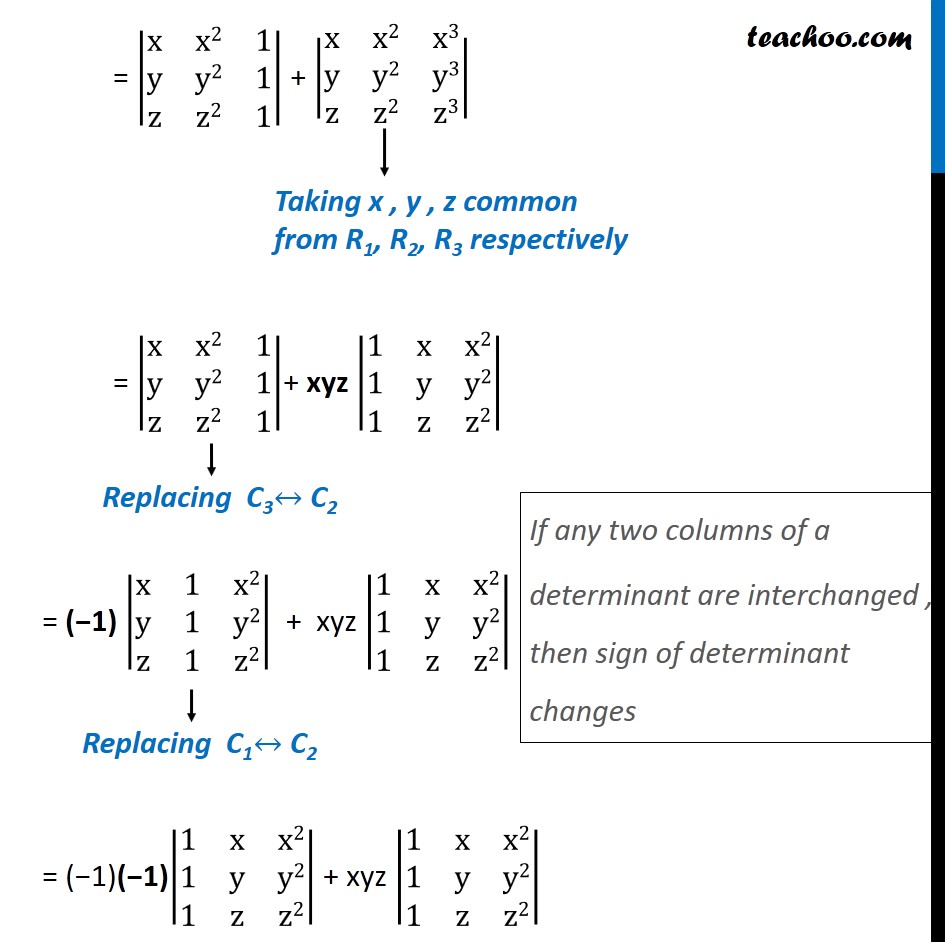
Question 10 If x, y, z are different and Δ = |■8(x&x2&1+x3@y&y2&1+y3@z&z2&1+z3)| = 0 , then show that 1 + xyz = 0 Solving ∆ = |■8(x&x2&1+x3@y&y2&1+y3@z&z2&1+z3)| Here, expanding elements of C3 into two determinants = |■8(x&x2&1@y&y2&1@z&z2&1)| + |■8(x&x2&x3@y&y2&y3@z&z2&z3)| = |■8(x&x2&1@y&y2&1@z&z2&1)| + |■8(x&x2&x3@y&y2&y3@z&z2&z3)| = |■8(x&x2&1@y&y2&1@z&z2&1)|+ xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = (−1) |■8(x&1&x2@y&1&y2@z&1&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = (−1)(−1)|■8(1&x&x2@1&y&y2@1&z&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| Taking x , y , z common from R1, R2, R3 respectively Replacing C3↔ C2 Replacing C1↔ C2 If any two columns of a determinant are interchanged , then sign of determinant changes = |■8(1&x&x2@1&y&y2@1&z&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = |■8(1&x&x2@1&y&y2@1&z&z2)| (1 + xyz) Using R2 → R2 – R1 and R3 → R3 – R1 = |■8(1&x&x2@𝟏 −𝟏&y−x&y2 −x2@𝟏−𝟏&z−x&z2 −x2)| (1+ xyz) = |■8(1&x&x2@𝟎&(y−x)&(y −x)(y+x)@𝟎&(z−x)&(z −x)(z+x))| (1+ xyz) Taking common factor (y – x) from R2 & (z – x) from R3 = (1 + xyz) (y – x) (z – x) |■8(1&x&x2@0&1&y+x@0&1&z+x)| Expanding determinant = (1 + xyz) (y – x) (z – x) (z – y) (1|■8(1&𝑦+𝑥@1&𝑧+𝑥)|" – 0 " |■8(𝑥&𝑥2@1&𝑧+𝑥)|" + 0" |■8(𝑥&𝑥2@1&𝑦+𝑥)|) = (1 + xyz) (y – x) (z – x) (1 (y + x) – (y + x) + 0 + 0) = (1 + xyz) (y – x) (z – x) (z + y – y – x) = (1 + xyz) (y – x) (z – x) (z – y) ∴ ∆ = (1 + xyz) (y – x) (z – x) (z – y) Since ∆ = 0 given (1 + xyz) (y – x) (z – x) (z – y) = 0 Since it is given that x, y, z all are different, i.e., y – x ≠ 0, z – x ≠ 0, z – y ≠ 0, So, only Possibility is (1 + xyz) = 0 Hence Proved