Ex 7.2, 8 - Chapter 7 Class 10 Coordinate Geometry (Term 1)

Transcript

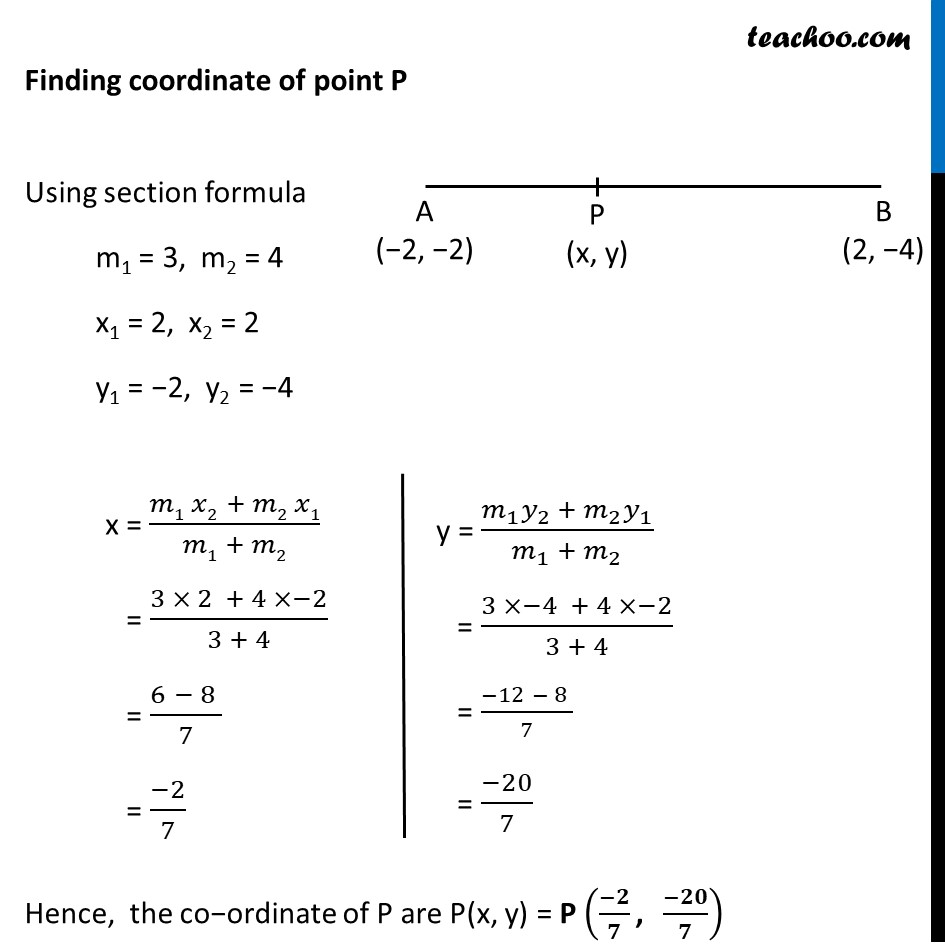
Ex 7.2, 8 If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that AP = 3/7 AB & P lies on the line segment AB. Let the co−ordinates of point P be P(x, y) It is given that AP = 3/7 (AB) AP = 3/7 (AP + PB) 7AP = 3AP + 3PB 7AP − 3AP = 3PB 4AP = 3PB 𝐴𝑃/𝑃𝐵 = 3/4 Hence the point P divides AB in the ratio of 3:4 Finding coordinate of point P Using section formula m1 = 3, m2 = 4 x1 = 2, x2 = 2 y1 = −2, y2 = −4 Hence, the co−ordinate of P are P(x, y) = P ((−𝟐)/𝟕 ", " (−𝟐𝟎)/𝟕) x = (𝑚1 𝑥2 + 𝑚2 𝑥1)/(𝑚1 + 𝑚2) = (3 × 2 + 4 ×−2)/(3 + 4) = (6 − 8 )/7 = (−2)/7 y = (𝑚_1 𝑦_2 + 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 ) = (3 ×−4 + 4 ×−2)/(3 + 4) = (−12 − 8 )/7 = (−20)/7