Example 2 - Chapter 3 Class 10 Pair of Linear Equations in Two Variables
Last updated at Dec. 13, 2024 by Teachoo
Examples
Example 1
Important
You are here
You are here
Chapter 3 Class 10 Pair of Linear Equations in Two Variables
Serial order wise
Transcript
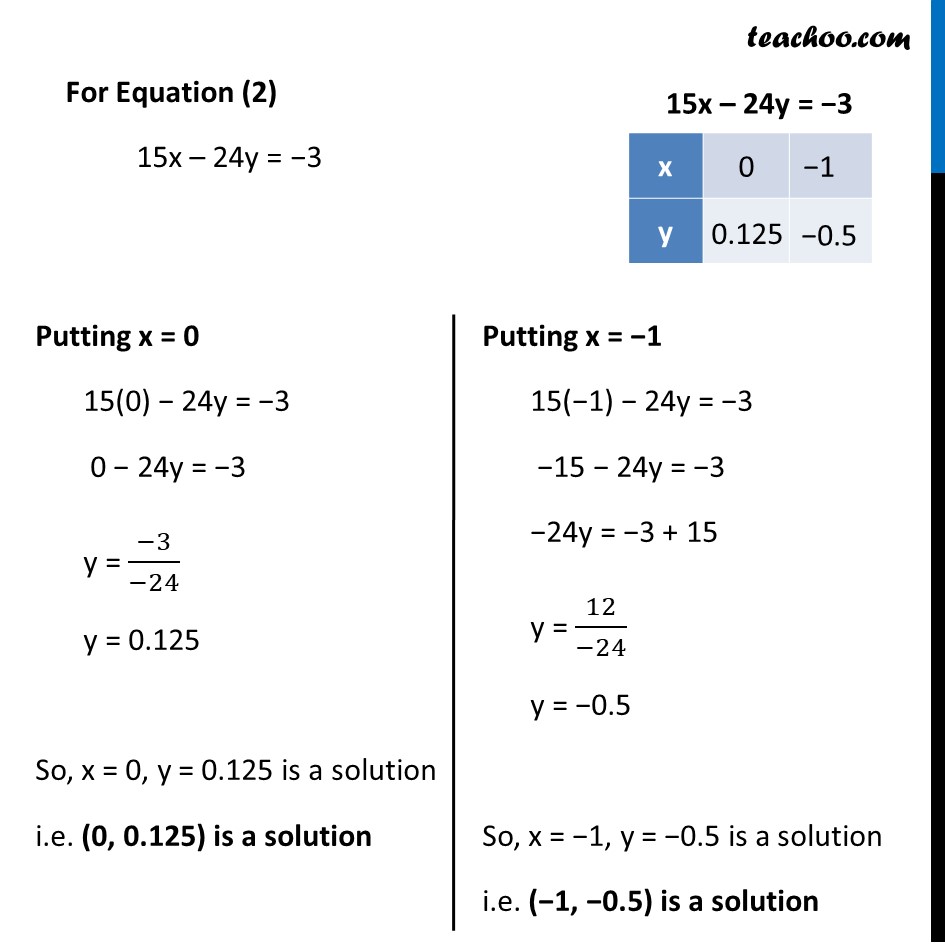
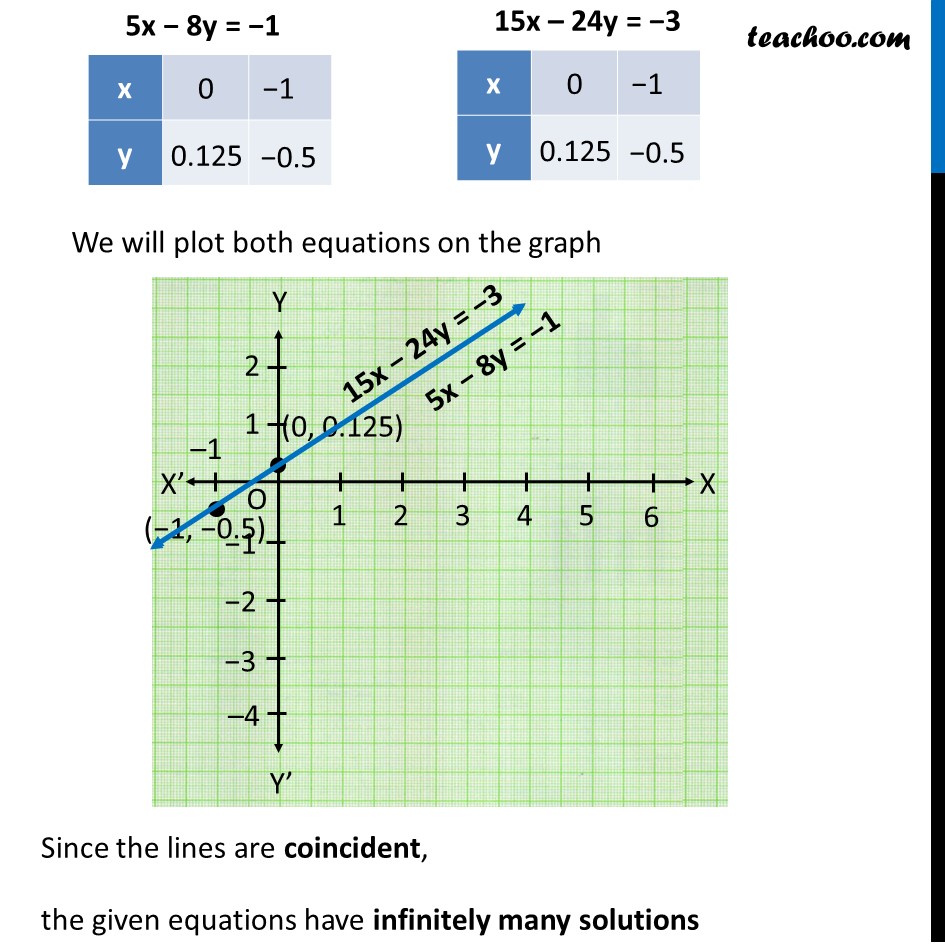
Putting x = 0 5(0) − 8y = −1 0 − 8y = −1 y = (−1)/(−8) y = 0.125 So, x = 0, y = 0.125 is a solution i.e. (0, 0.125) is a solution Putting x = −1 5(−1) − 8y = −1 −5 − 8y = −1 −8y = −1 + 5 y = 4/(−8) y = −0.5 So, x = −1, y = −0.5 is a solution i.e. (−1, −0.5) is a solution Putting x = 0 15(0) − 24y = −3 0 − 24y = −3 y = (−3)/(−24) y = 0.125 So, x = 0, y = 0.125 is a solution i.e. (0, 0.125) is a solution Putting x = −1 15(−1) − 24y = −3 −15 − 24y = −3 −24y = −3 + 15 y = 12/(−24) y = −0.5 So, x = −1, y = −0.5 is a solution i.e. (−1, −0.5) is a solution We will plot both equations on the graph Since the lines are coincident, the given equations have infinitely many solutions
