

Last updated at Feb. 14, 2025 by Teachoo




Transcript
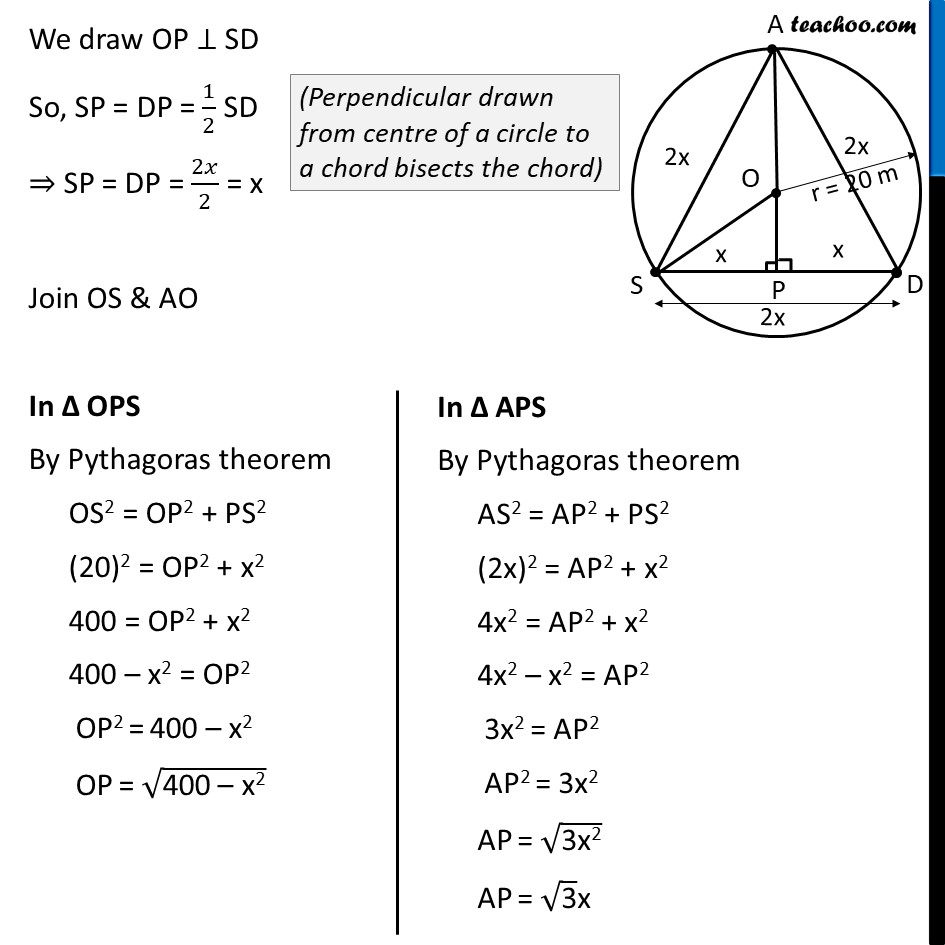
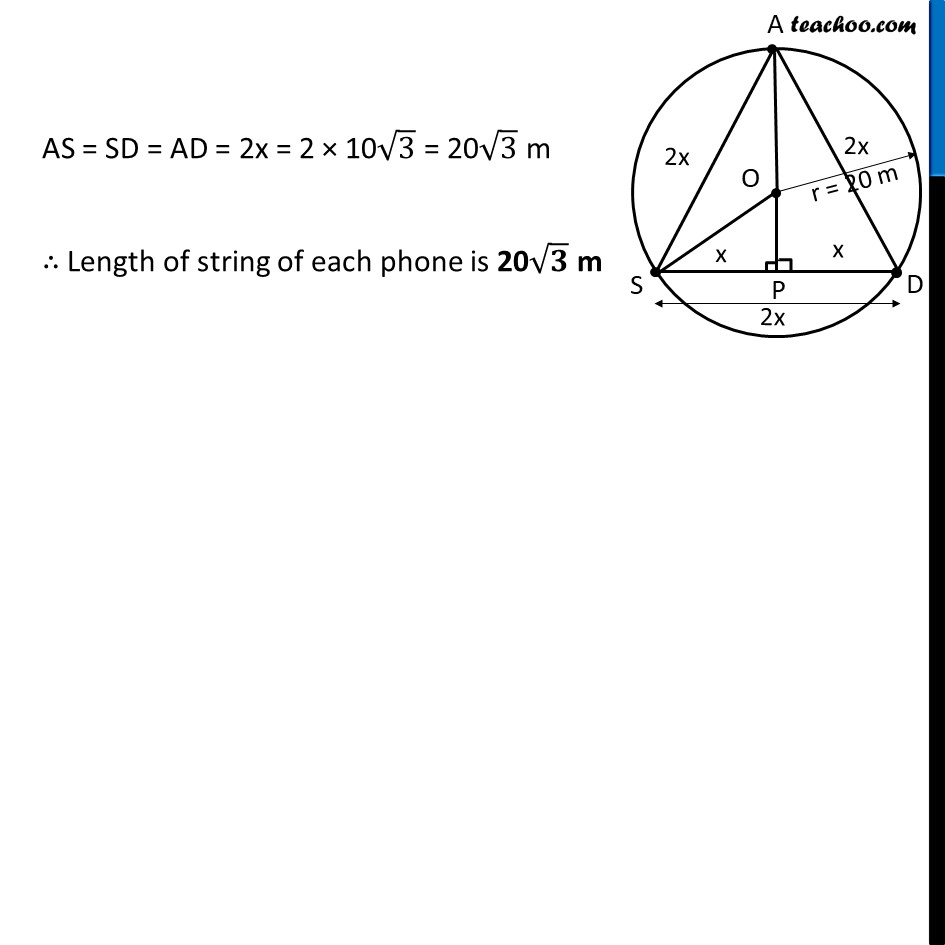
Ex 9.2, 6 A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone. Given: Circular park with radius 20m Let Ankur, Syed and David be donated by points A,S & D resp. Given all three are sitting at equal distances, i.e., AS = SD = AD To find: Length of AS = SD = AD Explanation: Let AS = SD = AD = 2x In ASD, all sides are equal, ∴ ASD is an equilateral triangle We draw OP ⊥ SD So, SP = DP = 1/2 SD ⇒ SP = DP = 2𝑥/2 = x Join OS & AO In Δ OPS By Pythagoras theorem OS2 = OP2 + PS2 (20)2 = OP2 + x2 400 = OP2 + x2 400 – x2 = OP2 OP2 = 400 – x2 OP = √("400 – x2" ) Now, AP = AO + OP √("3" )x = 20 + √("400 – x2" ) √("3" )x – 20 = √("400 – x2" ) √("400 – x2" ) = √("3" )x – 20 Squaring both sides (√("400 – x2" ))^2= (√("3" )x – 20)2 400 – x2 = (√3x)2 + (20)2 – 2 ×(√3x) × (20) "400 – x2 =" 3x2 + 400 – 40√3x "400 – 400 + 40" √3 "x =" 3x2 + x2 "40" √3 "x =" 4x2 4x2 = 40√3x "x2" /"x" = 40/4 √3 x = 10√3 m AS = SD = AD = 2x = 2 × 10√3 = 20√3 m ∴ Length of string of each phone is 20√3 m