
Last updated at Feb. 27, 2025 by Teachoo


Transcript
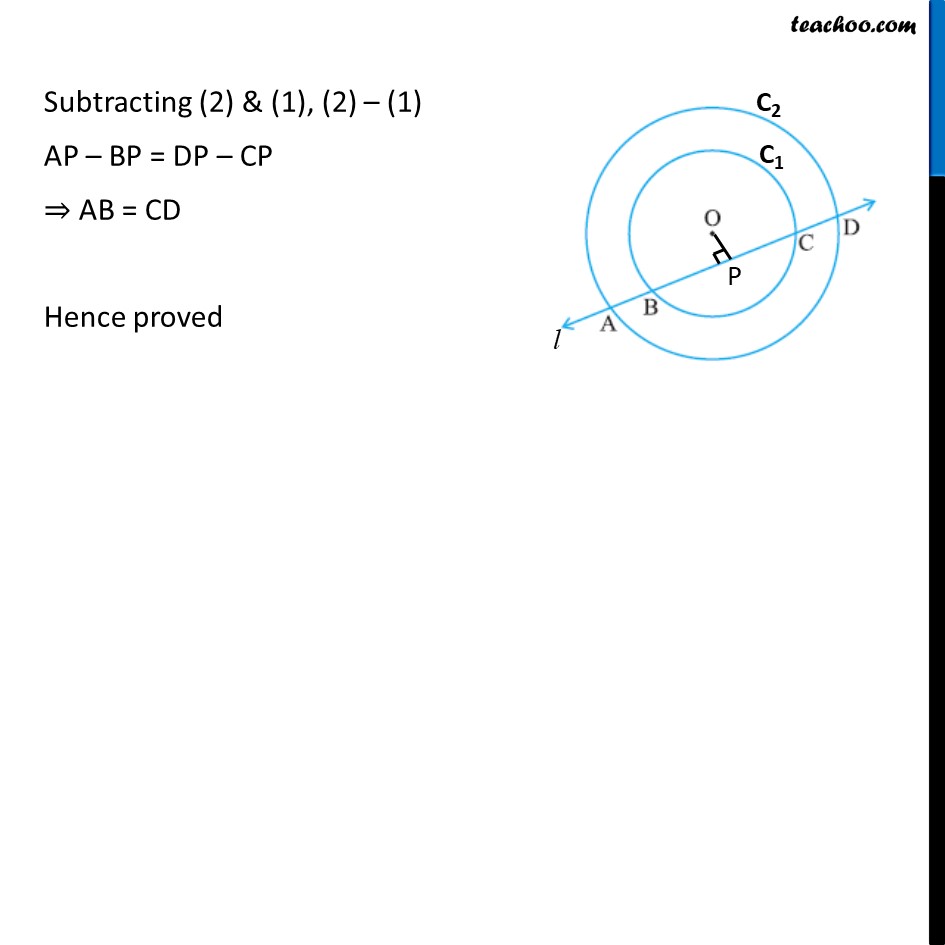
Ex 9.2, 4 If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see figure). Given: Two concentric circles with centre O. & a line intersects the circles at A,B,C & D To prove: AB = CD Proof: Let two circles be C1 & C2 and line be l We draw OP perpendicular to line l In circle C1, OP ⊥ BC So, OP bisects BC, i.e. BP = CP (As OP is perpendicular to line l ) (Perpendicular drawn from centre of a circle to a chord bisects the chord) In circle C2, OP ⊥ AD So, OP bisects AD, i.e. AP = DP (As OP is perpendicular to line l ) (Perpendicular drawn from centre of a circle to a chord bisects the chord) Subtracting (2) & (1), (2) – (1) AP – BP = DP – CP ⇒ AB = CD Hence proved