Last updated at April 16, 2024 by Teachoo


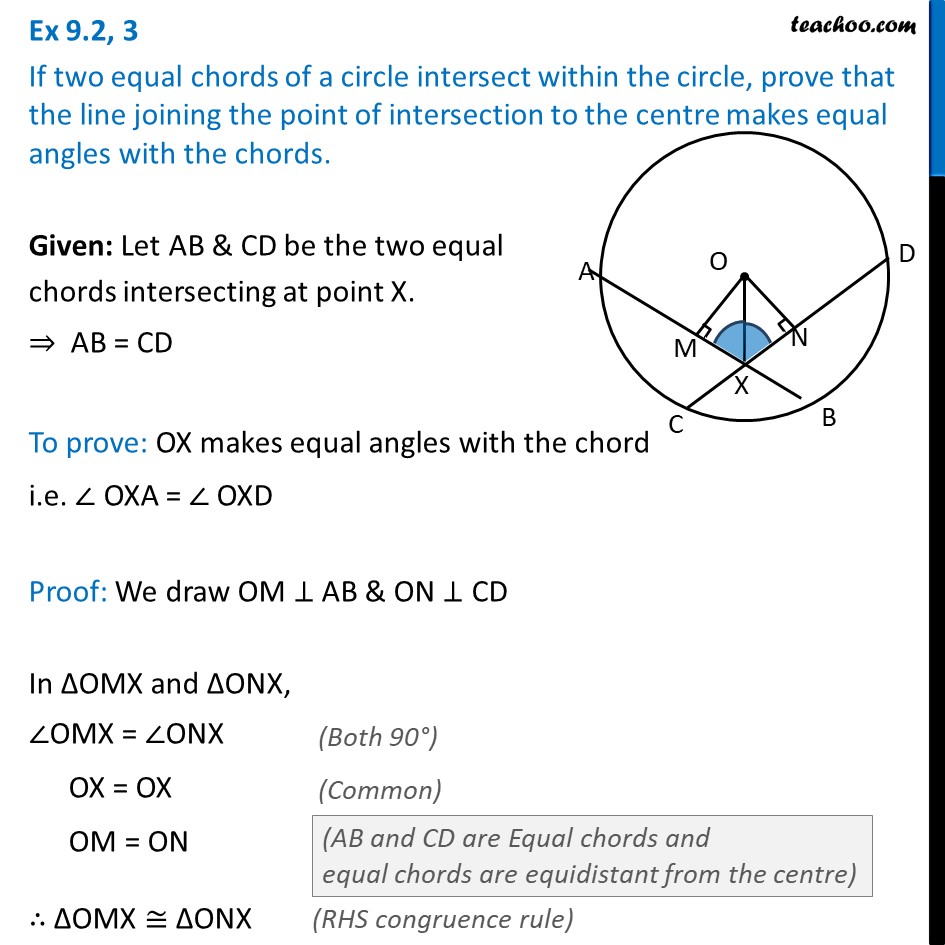
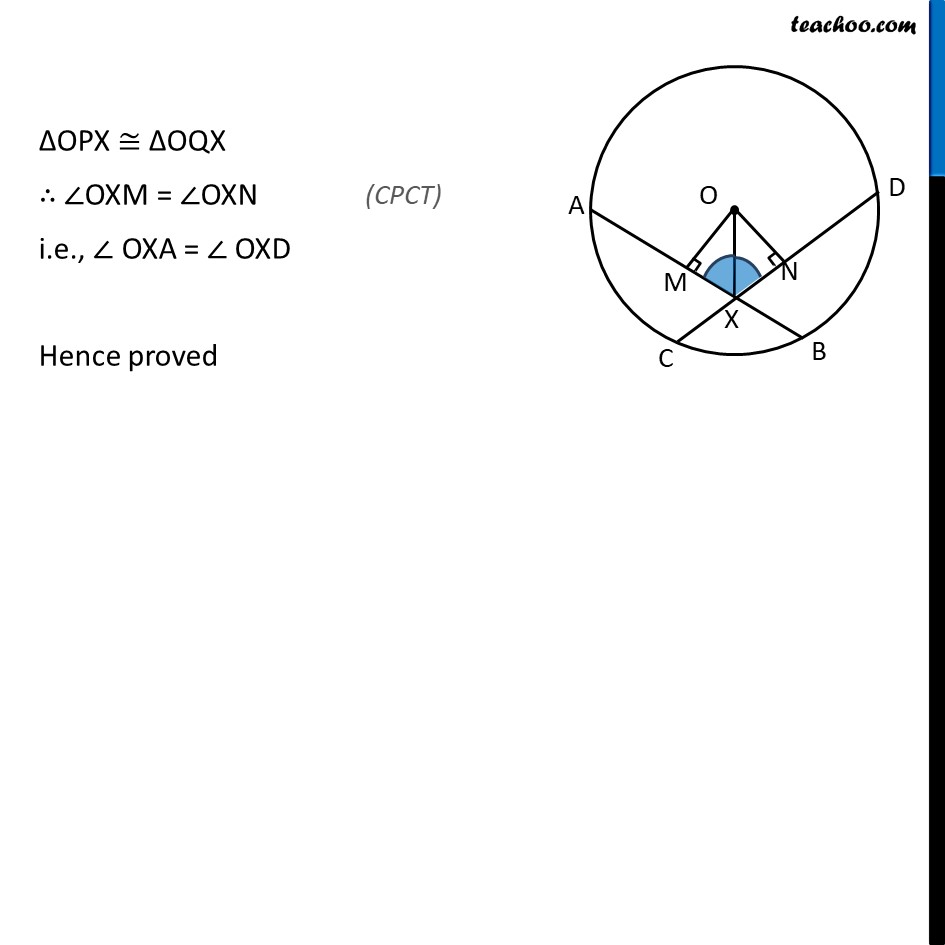
Ex10.4, 3 If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords. Given: Let AB & CD be the two equal chords intersecting at point X. ⇒ AB = CD To prove: OX makes equal angles with the chord i.e. ∠ OXA = ∠ OXD Proof: We draw OM ⊥ AB & ON ⊥ CD In ΔOMX and ΔONX, ∠OMX = ∠ONX OX = OX OM = ON ∴ ΔOMX ≅ ΔONX ΔOPX ≅ ΔOQX ∴ ∠OXM = ∠OXN i.e., ∠ OXA = ∠ OXD Hence proved