Triple angle formulas

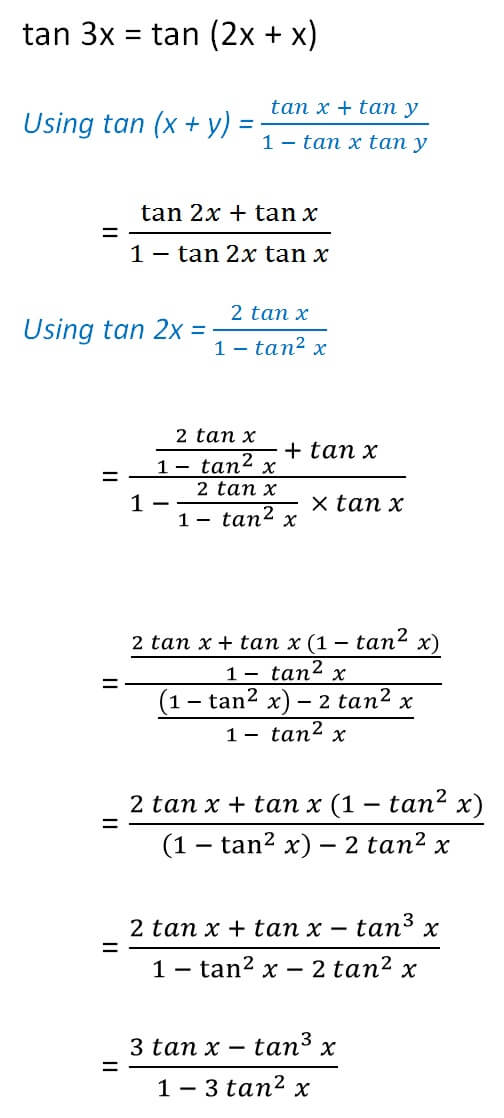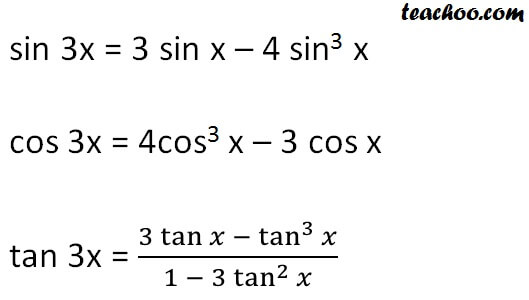
These formulas can be derived using x + y formulas

For sin 3x

sin 3x = sin (2x + x)

Using sin (x + y) = sin x cos y + cos x sin y

   = sin 2x cos x + sin x cos 2x

Using cos 2x = 1 – 2 sin ² x and sin 2x = 2 sin x cos x

   = (2 sin x cos x) cos x + sin x (1 – 2sin ² x)

   = 2 sin x cos ² x + sin x – 2sin ³ x

Using cos ² x = 1 – sin ² x

   = 2 sin x (1 – sin ² x) + sin x – 2sin ³ x)

   = 2 sin x – 2sin ³ x + sin x – 2sin ³ x

   = 3 sin x – 4 sin ³ x

For cos 3 x

cos 3x = cos (2x + x)

Using cos (x + y) = cos x cos y – sin x sin y

   = cos 2x cos x – sin 2x sin x

Using cos 2x = 2 cos ² x – 1 and sin 2x = 2 sin x cos x

   = (2cos ² x – 1) cos x – (2 sin x cos x) sin x

   = 2cos ² x – cos x – 2 sin ² x cos x

Using sin ² x = 1 – cos ² x

   = 2cos ³ x – cos x – 2 (1 – cos ² x) cos x

   = 2cos ³ x – cos x – 2 cos x (1 – cos ² x)

   = 2cos ³ x – cos x – 2 cos x + 2 cos ³ x

   = 4cos ³ x – 3cos x

For tan 3x