Question 2 - Chapter 12 Class 12 Linear Programming (Important Question)

Transcript

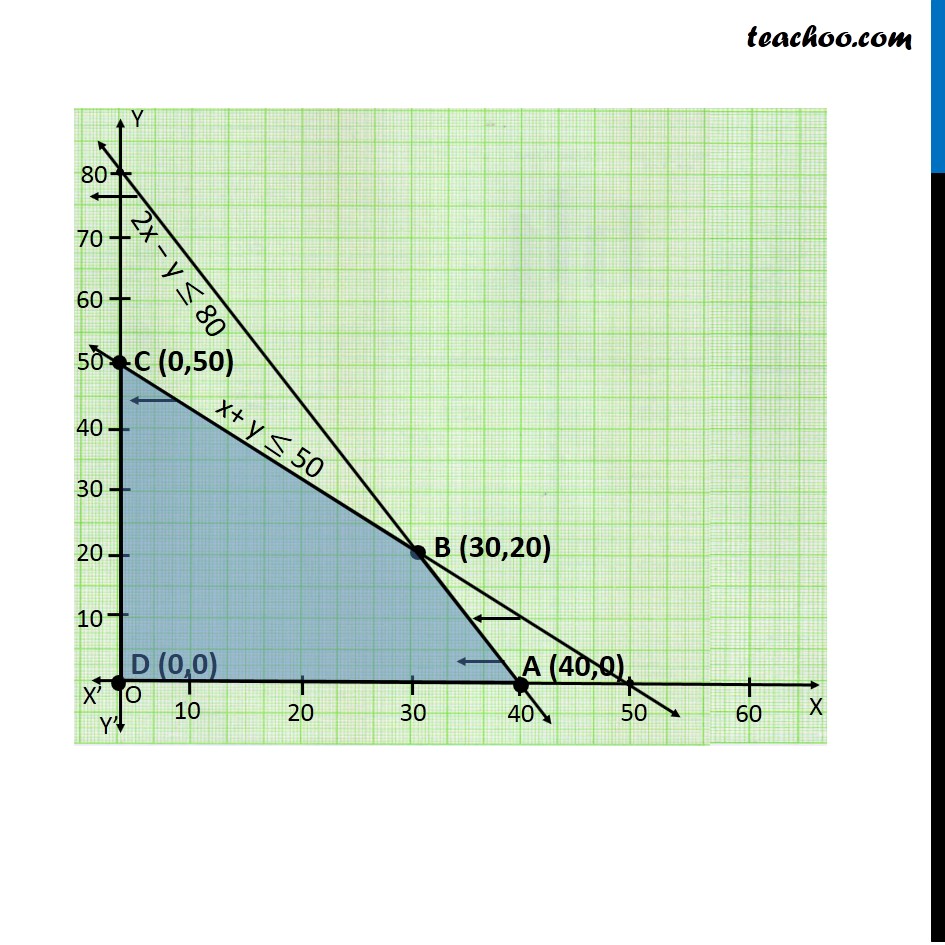
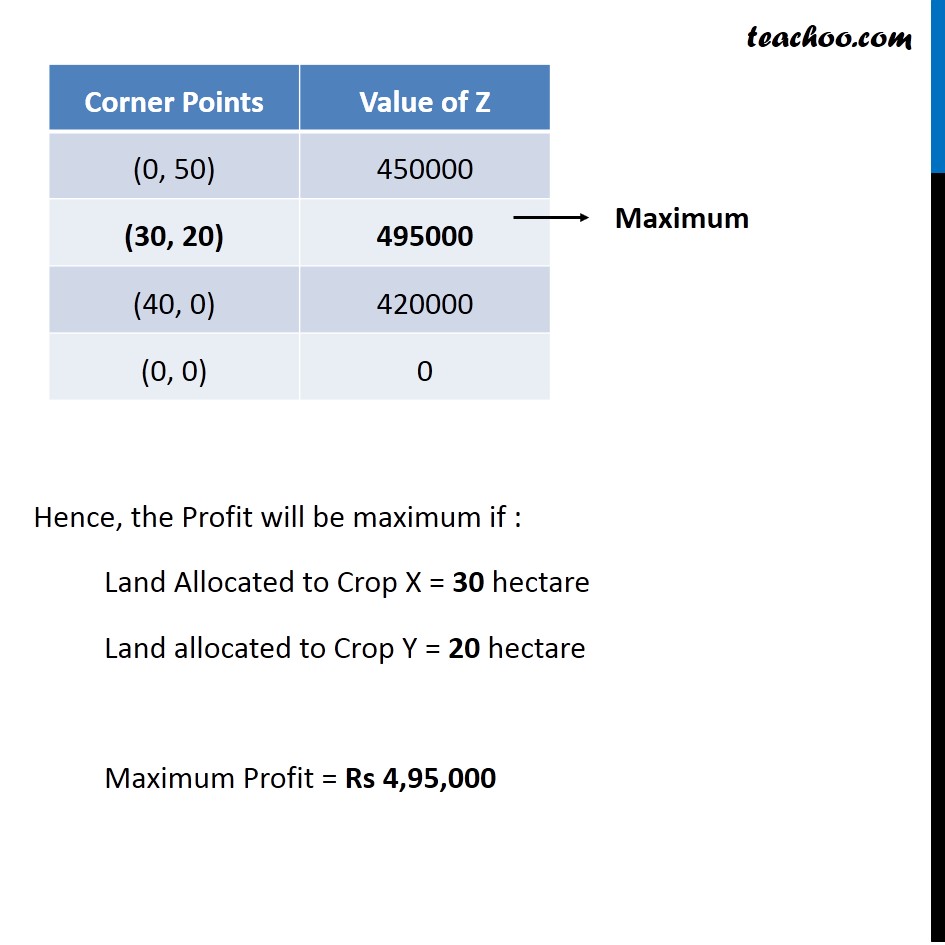
Question 2 A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at rates of 20 litres and 10 litres per hectare. Further, no more than 800 litres of herbicide should be used in order to protect fish and wild life using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?Let the land allocated to Crop X be x hectare and land allocated to crop Y be y hectare According to Question : Herbicide used for crop X = 20 litres per hectare Herbicide used for crop Y = 10 litres per hectare Maximum quantity of herbicide = 800 litres ∴ 20x + 10y ≤ 800 2x + y ≤ 800 Also, Total land Available to grow crops = 50 hectare ∴ x + y ≤ 50 As we want to Maximize the Profit Hence, the function used here is Maximize Z. Profit from crop X = Rs 10500 per hectare Profit from crop Y = Rs 9000 per hectare Maximize Z = 10500 x + 9000 y Combining all constraints : Maximize Z = 10500 x + 9000 y Subject to Constraints : 2x + y ≤ 80 x + y ≤ 50 x, y ≥ 0 Hence, the Profit will be maximum if : Land Allocated to Crop X = 30 hectare Land allocated to Crop Y = 20 hectare Maximum Profit = Rs 4,95,000