Question 7 - Solving Pair of Linear Inequalities - Chapter 5 Class 11 Linear Inequalities

Transcript

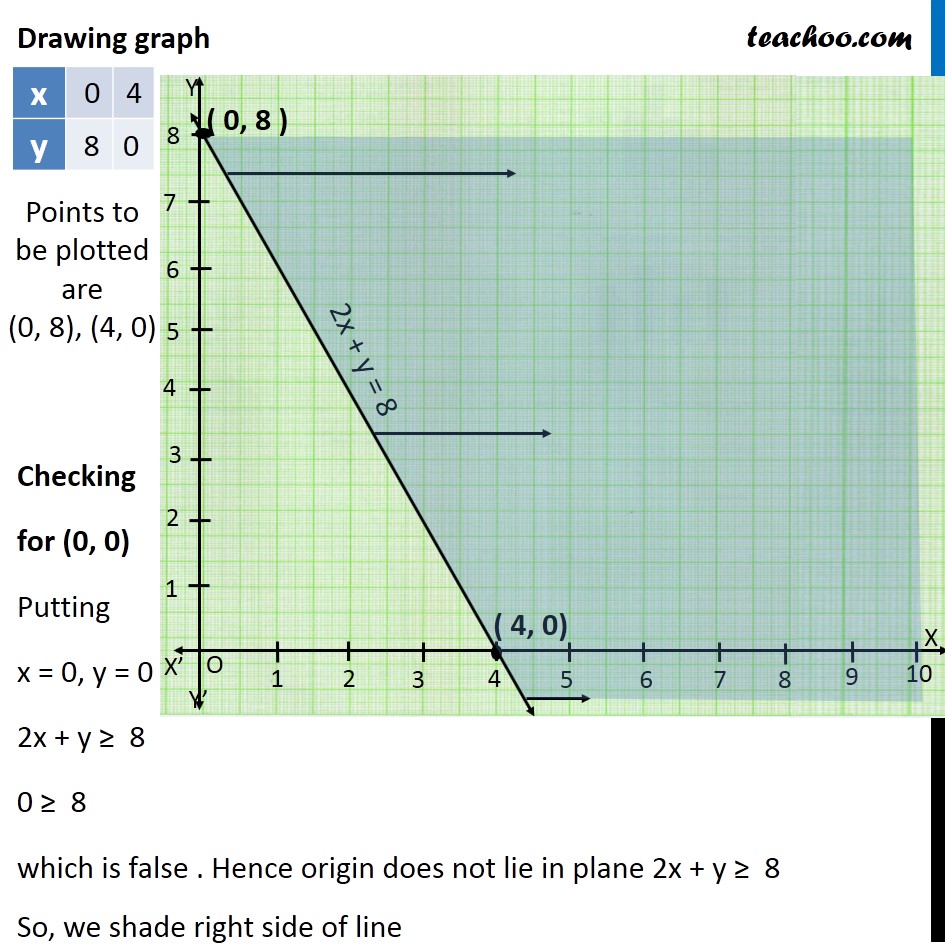
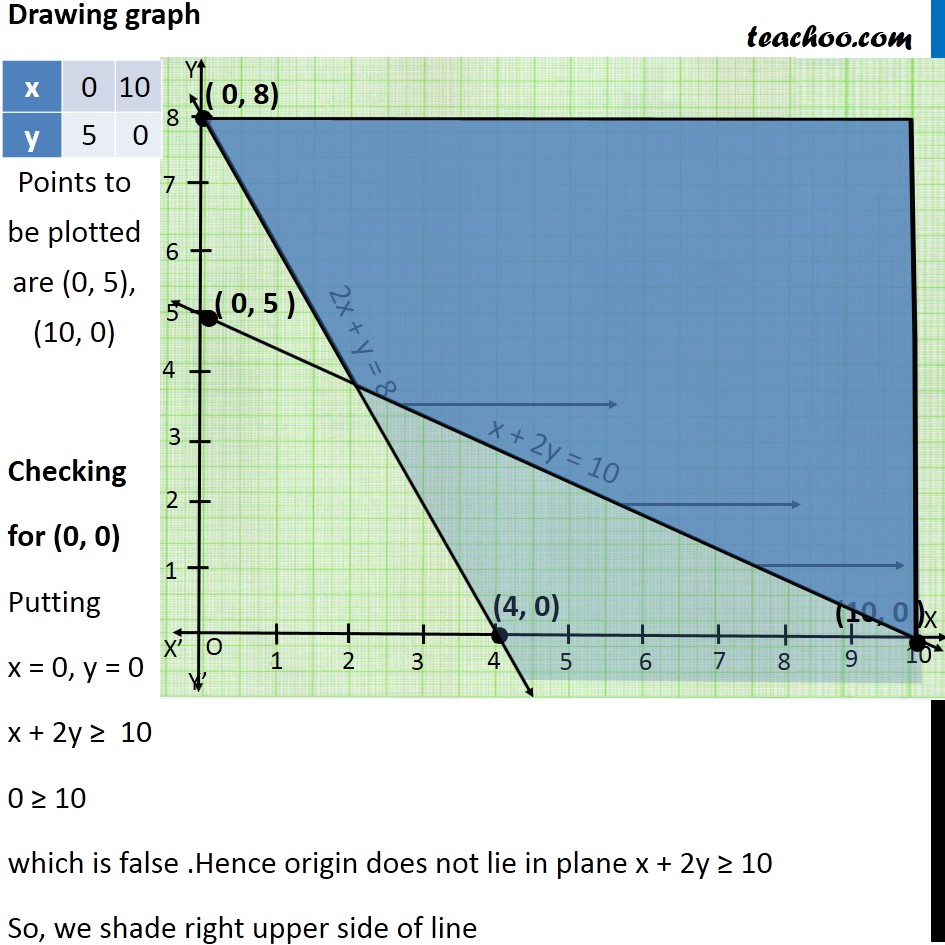
Question 7 Solve the following system of inequalities graphically: 2x + y ≥ 8, x + 2y ≥ 10 First we solve 2x + y ≥ 8 Lets first draw graph of 2x + y = 8 Putting x = 0 in (1) 2(0) + y = 6 0 + y = 6 y = 8 Putting y = 0 in (1) 2x + (0) = 6 2x = 8 x = 8/2 x = 4 Points to be plotted are (0, 8), (4, 0) Drawing graph Checking for (0, 0) Putting x = 0, y = 0 2x + y ≥ 8 0 ≥ 8 which is false . Hence origin does not lie in plane 2x + y ≥ 8 So, we shade right side of line First we solve x + 2y ≥ 10 Lets first draw graph of x + 2y = 10 Putting x = 0 in (1) 0 + 2y = 10 2y = 10 y = 10/2 y = 5 Putting y = 0 in (1) x + 2(0) = 10 x + 0 = 10 x = 10 Points to be plotted are (0, 5), (10, 0) Drawing graph Checking for (0, 0) Putting x = 0, y = 0 x + 2y ≥ 10 0 ≥ 10 which is false .Hence origin does not lie in plane x + 2y ≥ 10 So, we shade right upper side of line