Ex 13.3, 6 - Chapter 13 Class 12 Probability

Transcript

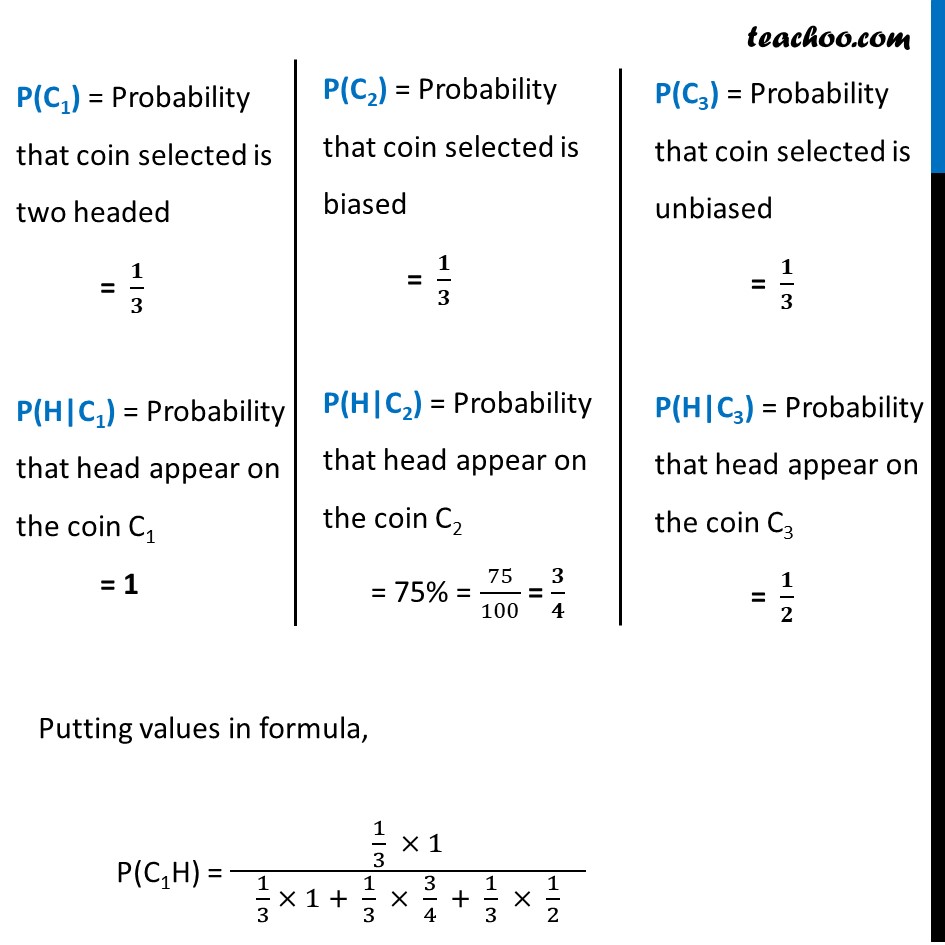
Ex 13.3, 6 There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin ? Let C1 : Two headed coin C2 : Biased coin C3 : Unbiased coin H : Head appears on the coin We need to find the Probability that coin is two headed, if it shows head i.e. P(C1|H) P(C1|H) = (𝑃(𝐶_1 ).𝑃(𝐻|𝐶_1))/(𝑃(𝐶_1 ).𝑃(𝐻|𝐶_1)+𝑃(𝐶_2 ).𝑃(𝐻|𝐶_2)+𝑃(𝐶_3 ).𝑃(𝐻|𝐶_3)) "P(C1)" = Probability that coin selected is two headed = 𝟏/𝟑 "P(H|C1)" = Probability that head appear on the coin C1 = 1 "P(C2)" = Probability that coin selected is biased = 𝟏/𝟑 "P(H|C2)" = Probability that head appear on the coin "C2" = 75% = 75/100 = 𝟑/𝟒 "P(C3)" = Probability that coin selected is unbiased = 𝟏/𝟑 "P(H|C3)" = Probability that head appear on the coin "C3" = 𝟏/𝟐 Putting values in formula, P(C1|H) = (1/3 × 1)/(1/3 × 1 + 1/3 × 3/4 + 1/3 × 1/2 ) = (1/3 × 1)/( 1/3 [1 + 3/4 + 1/2 ] ) = 1/( 9/4 ) = 𝟒/𝟗 Therefore, required probability is 𝟒/𝟗