Ex 1.3 , 6 - Chapter 1 Class 12 Relation and Functions

Transcript

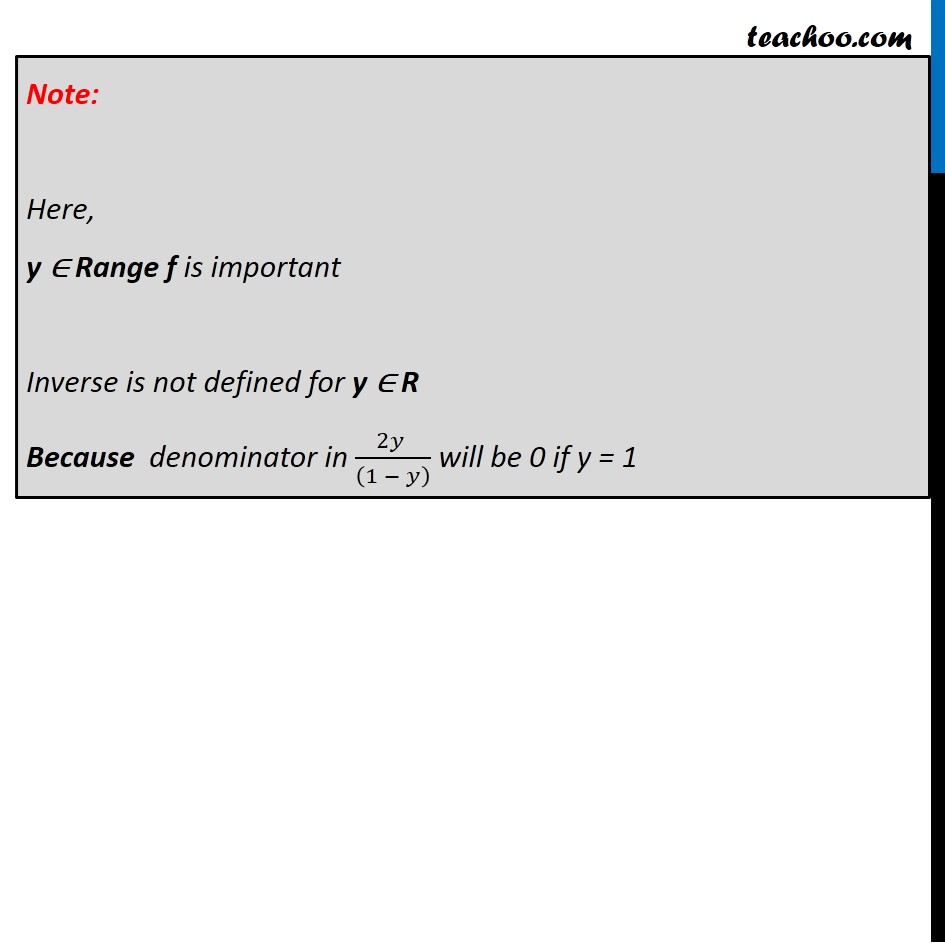
Ex 1.3, 6 Show that f: [−1, 1] → R, given by f(x) = 𝑥/(𝑥 + 2) is one-one. Find the inverse of the function f: [−1, 1] → Range f. (Hint: For y ∈ Range f, y = f(x) = 𝑥/(𝑥 + 2) , for some x in [−1, 1], i.e., x = 2𝑦/(1 − 𝑦) ) f(x) = x/(x+2) Check one-one f(x1) = 𝑥1/(𝑥1 + 2) f(x2) = 𝑥2/(𝑥2 + 2) Rough One-one Steps: 1. Calculate f(x1) 2. Calculate f(x2) 3. Putting f(x1) = f(x2) we have to prove x1 = x2 Putting f(x1) = f(x2) 𝑥1/(𝑥1 + 2) = 𝑥2/(𝑥2 + 2) x1(x2 + 2) = x2(x1 + 2) x1x2 + 2x1 = x2x1 + 2x2 x1x2 – x2x1 + 2x1 = 2x2 0 + 2x1 = 2x2 2x1 = 2x2 x1 = x2 Hence, if f(x1) = f(x2) , then x1 = x2 ∴ f is one-one Checking onto f(x) = 𝑥/(𝑥 + 2) Putting f(x) = y y = 𝑥/(𝑥 + 2) y(x + 2) = x yx + 2y = x yx – x = –2y x(y – 1) = –2y x = (−2𝑦 )/(𝑦 −1) x = (−2𝑦 )/(−1(−𝑦 + 1) ) x = (2𝑦 )/((1 − 𝑦) ) Now, Checking for y = f(x) Putting value of x in f(x) f(x) = f((2𝑦 )/((1 − 𝑦) )) = ((2𝑦 )/((1 − 𝑦) ))/((2𝑦 )/((1 − 𝑦) ) + 2) = ((2𝑦 )/((1 − 𝑦) ))/((2𝑦 + 2(1 − 𝑦) )/((1 − 𝑦) )) = 2𝑦/(2𝑦 + 2 − 2𝑦) = y Thus, for every y ∈ Range f, there exists x ∈ [−1, 1] such that f(x) = y Hence, f is onto Since f(x) is one-one and onto, So, f(x) is invertible And Inverse of x = 𝑓^(−1) (𝑦) = (2𝑦 )/((1 − 𝑦) ) , y ≠ 1 Note: Here, y ∈ Range f is important Inverse is not defined for y ∈ R Because denominator in (2𝑦 )/((1 − 𝑦) ) will be 0 if y = 1