Question 11 - Chapter 8 Class 12 Application of Integrals (Important Question)

Transcript

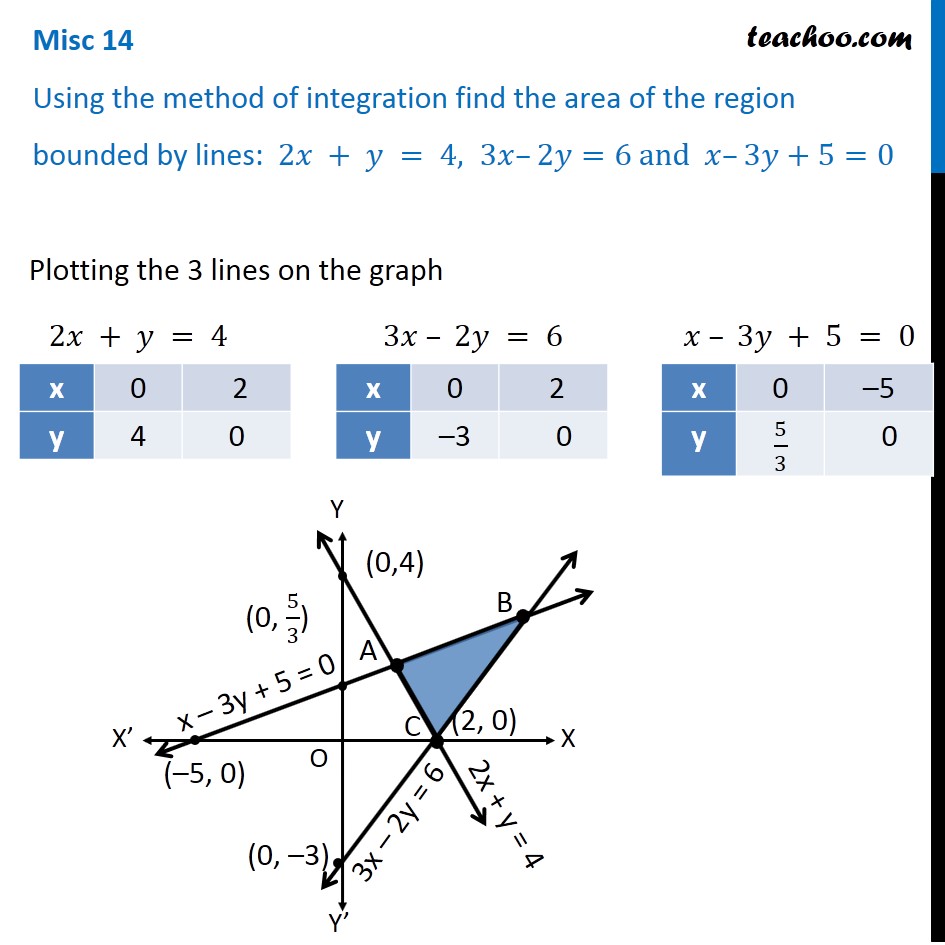
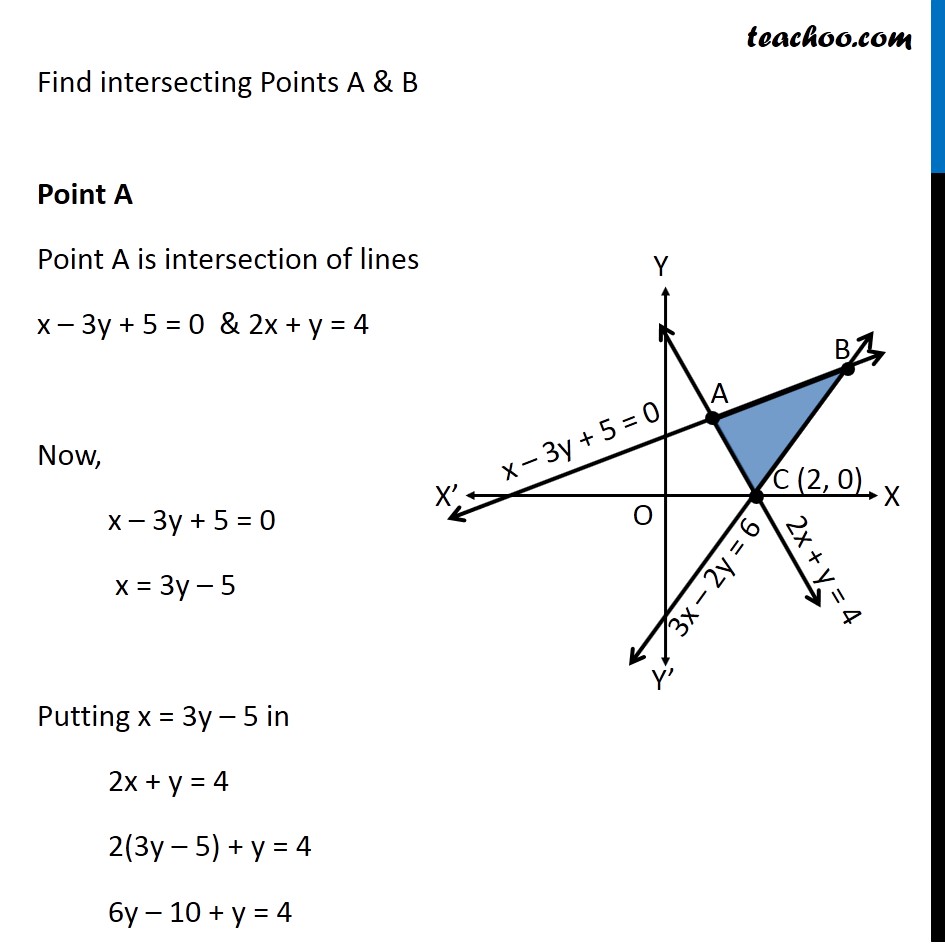
Question 11 Using the method of integration find the area of the region bounded by lines: 2𝑥 + 𝑦 = 4, 3𝑥–2𝑦=6 and 𝑥–3𝑦+5=0 Plotting the 3 lines on the graph 2𝑥 + 𝑦 = 4 3𝑥 – 2𝑦 = 6 𝑥 – 3𝑦 + 5 = 0 Find intersecting Points A & B Point A Point A is intersection of lines x – 3y + 5 = 0 & 2x + y = 4 Now, x – 3y + 5 = 0 x = 3y – 5 Putting x = 3y – 5 in 2x + y = 4 2(3y – 5) + y = 4 6y – 10 + y = 4 7y = 14 y = 2 Putting y = 2 in x – 3y + 5 = 0 x – 3(2) + 5 = 0 x – 6 + 5 = 0 x = 1 So, point A (1, 2) Point B Point B is intersection of lines x – 3y + 5 = 0 & 3x – 2y = 6 Now, x – 3y + 5 = 0 x = 3y – 5 Putting x = 3y – 5 in 3x – 2y = 6 3(3y – 5) – 2y = 6 9y – 15 – 2y = 6 7y = 21 y = 3 Putting y = 3 in x – 3y + 5 = 0 x – 3(3) + 5 = 0 x – 9 + 5 = 0 x = 4 So, point B is (4, 3) Finding area Area Required = Area ABED – Area ACD – Area CBE Area ABED Area ABED =∫_1^4▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of AB 𝑥 – 3𝑦+5=0 𝑥+5=3𝑦 (𝑥 + 5)/3=𝑦 𝑦=(𝑥 + 5)/3 Therefore, Area ABED =∫_1^4▒〖((𝑥+5)/3) 𝑑𝑥〗 =1/3 ∫_1^4▒〖(𝑥+5) 𝑑𝑥〗 =1/3 [𝑥^2/2+5𝑥]_1^4 =1/3 [4^2/2+5.4−[1^2/2+5.1]] =1/3 [8+20−1/2−5] =1/3 [45/2] =15/2 Area ACD Area ACD =∫_1^2▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of line AC 2𝑥+𝑦=4 𝑦=4−2𝑥 Area ACD =∫_1^2▒〖(4−2𝑥" " ) 𝑑𝑥〗 =[4𝑥−(2𝑥^2)/2]_1^2 =[4𝑥−𝑥^2 ]_1^2 =[4.2−2^2−[4.1−1^2 ]] =[8−4−4+1] = 1 Area CBE Area CBE =∫_2^4▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of line BC 3𝑥+2𝑦=6 3𝑥−6=2𝑦 (3𝑥 − 6)/2=𝑦 𝑦=(3𝑥 − 6)/2 Therefore, Area CBE =∫_2^4▒〖((3𝑥 − 6)/2) 𝑑𝑥〗 =1/2 ∫_2^4▒〖(3𝑥−6) 𝑑𝑥〗 =1/2 [(3𝑥^2)/2−6𝑥]_2^4 =1/2 [〖3.4〗^2/2−6.4−[〖3.2〗^2/2−6.2]] =1/2 [24−24−6+12] =3 Hence Area Required = Area ABED – Area ACD – Area CBE =15/2−1−3 =15/2−4 =(15 − 8)/2 =𝟕/𝟐 square units