

Ex 8.1
Ex 8.1, 2
Ex 8.1, 3 (MCQ)
Ex 8.1, 4 (MCQ) Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Important Deleted for CBSE Board 2024 Exams
Question 3 Deleted for CBSE Board 2024 Exams
Question 4 Important Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Deleted for CBSE Board 2024 Exams You are here
Last updated at April 16, 2024 by Teachoo



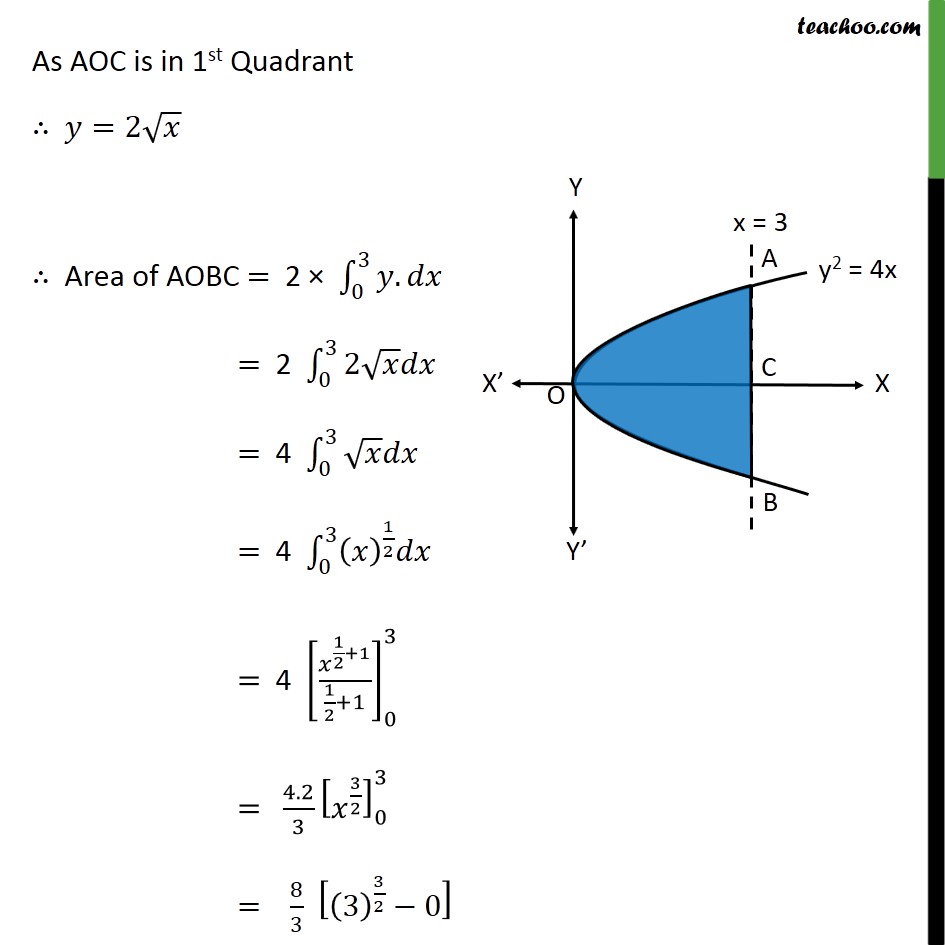
Question 9 Find the area of the region bounded by the curve 2=4 and the line =3 . Let AB represents the line =3 and AOB represent the curve 2 =4 Area of AOBC = 2 [Area of AOC] = 2 0 3 . We know that 2 =4 = 4 = 2 As AOC is in 1st Quadrant =2 Area of AOBC = 2 0 3 . = 2 0 3 2 = 4 0 3 = 4 0 3 1 2 = 4 1 2 +1 1 2 +1 0 3 = 4.2 3 3 2 0 3 = 8 3 3 3 2 0 = 8 3 3 3 2 0 = 8 3 3 3 = 8 3 3 3 3 = 8 3 3 3 = 8 3 Required Area = square units