Misc 7 - Chapter 3 Class 12 Matrices

Transcript

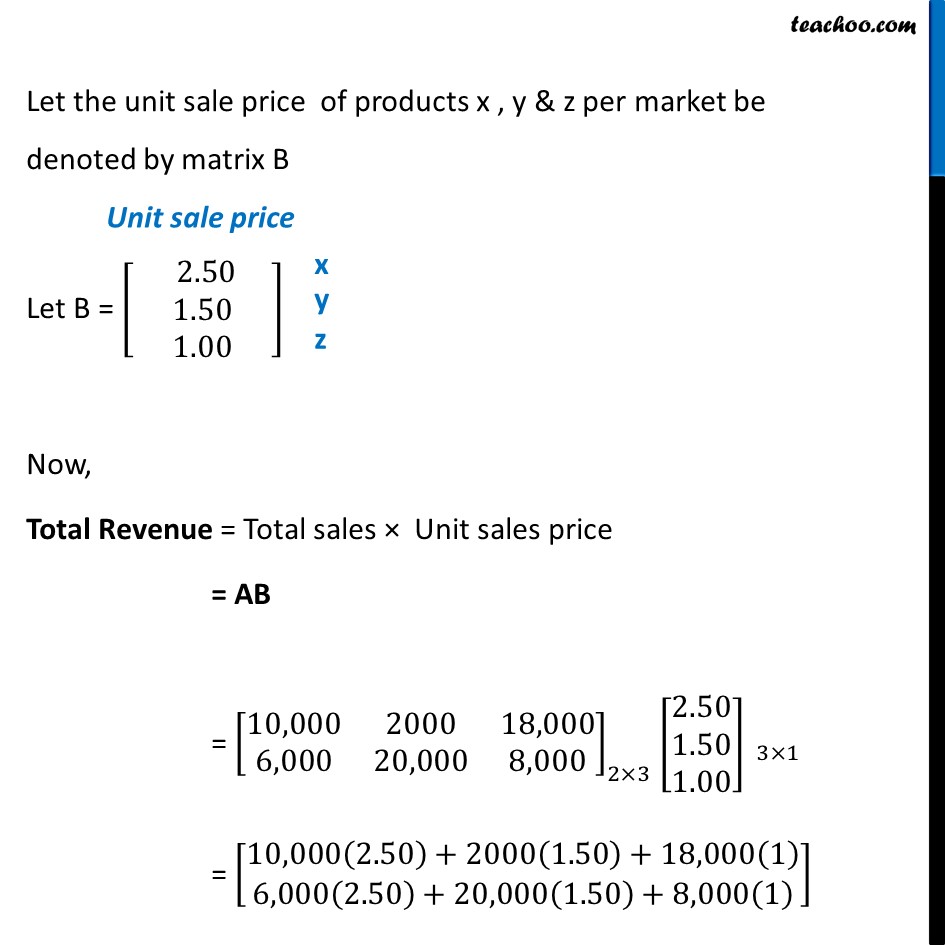
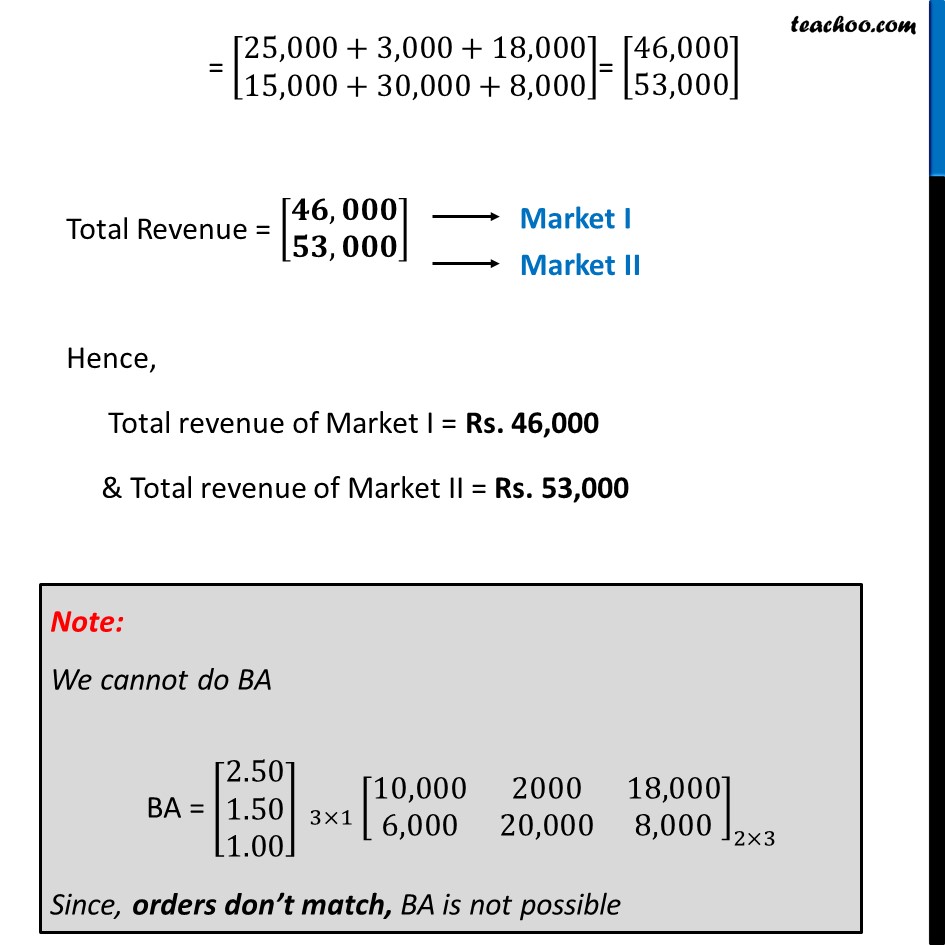
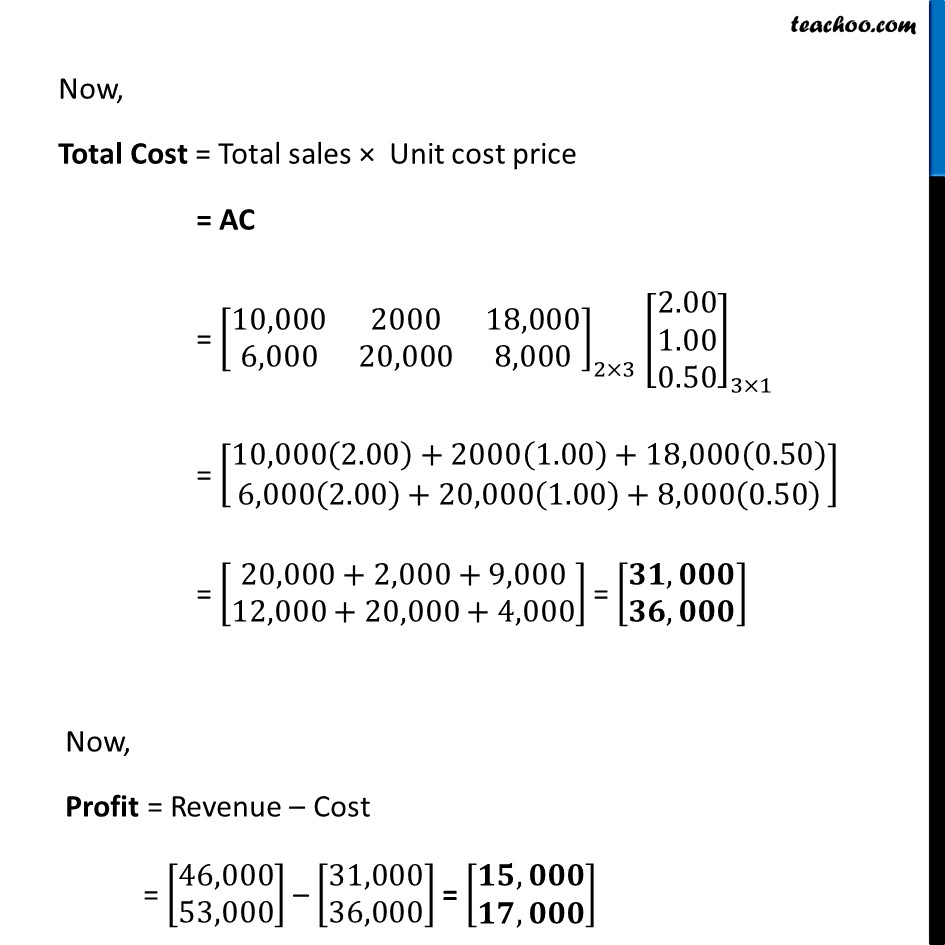
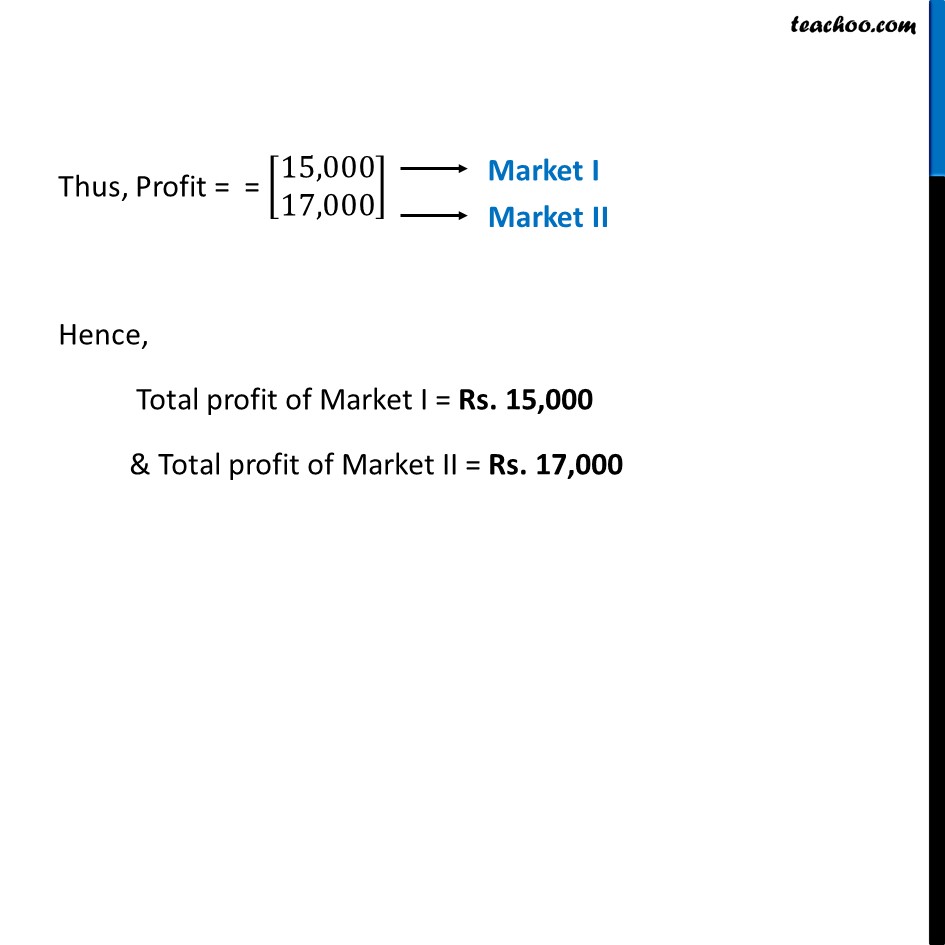
Misc 7 (a) A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below: Market Products I 10,000 2,000 18,000 II 6,000 20,000 8,000 (a) If unit sale prices of x, y and z are Rs 2.50, Rs 1.50 and Rs 1.00, respectively. Find the total revenue in each market with the help of matrix algebra. Let the sales of products x , y & z per market be denoted by matrix A A = [■8(10,000&2000&18,000@6,000&20,000&8,000)] Let the unit sale price of products x , y & z per market be denoted by matrix B Let B = [■8( 2.50 @1.50@1.00)] Now, Total Revenue = Total sales × Unit sales price = AB = [■8(10,000&2000&18,000@6,000&20,000&8,000)]_(2×3) [■8(2.50@1.50@1.00)]" " _(3×1) = [■8(10,000(2.50)+2000(1.50)+18,000(1)@6,000(2.50)+20,000(1.50)+8,000(1) )] = [■8(25,000+3,000+18,000@15,000+30,000+8,000)]= [■8(46,000@53,000)] Total Revenue = [■8(𝟒𝟔,𝟎𝟎𝟎@𝟓𝟑,𝟎𝟎𝟎)] Hence, Total revenue of Market I = Rs. 46,000 & Total revenue of Market II = Rs. 53,000 Note: We cannot do BA BA = [■8(2.50@1.50@1.00)]" " _(3×1) [■8(10,000&2000&18,000@6,000&20,000&8,000)]_(2×3) Since, orders don’t match, BA is not possible Misc 7 (b) A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below: Market Products I 10,000 2,000 18,000 II 6,000 20,000 8,000 (b) If the unit costs of the above three commodities are Rs 2.00, Rs 1.00 and 50 paise respectively. Find the gross profit. Let the unit cost price of products x , y & z per market be denoted by matrix C Let C = [■8( 2.00 @1.00@0.50)] Now, Total Cost = Total sales × Unit cost price = AC = [■8(10,000&2000&18,000@6,000&20,000&8,000)]_(2×3) [■8(2.00@1.00@0.50)]_(3×1) = [■8(10,000(2.00)+2000(1.00)+18,000(0.50)@6,000(2.00)+20,000(1.00)+8,000(0.50) )] = [■8(20,000+2,000+9,000@12,000+20,000+4,000)] = [■8(𝟑𝟏,𝟎𝟎𝟎@𝟑𝟔,𝟎𝟎𝟎)] Now, Profit = Revenue – Cost = [■8(46,000@53,000)] – [■8(31,000@36,000)] = [■8(𝟏𝟓,𝟎𝟎𝟎@𝟏𝟕,𝟎𝟎𝟎)] Thus, Profit = = [■8(15,000@17,000)] Hence, Total profit of Market I = Rs. 15,000 & Total profit of Market II = Rs. 17,000