Example 4 - Chapter 2 Class 12 Inverse Trigonometric Functions (Important Question)

Transcript

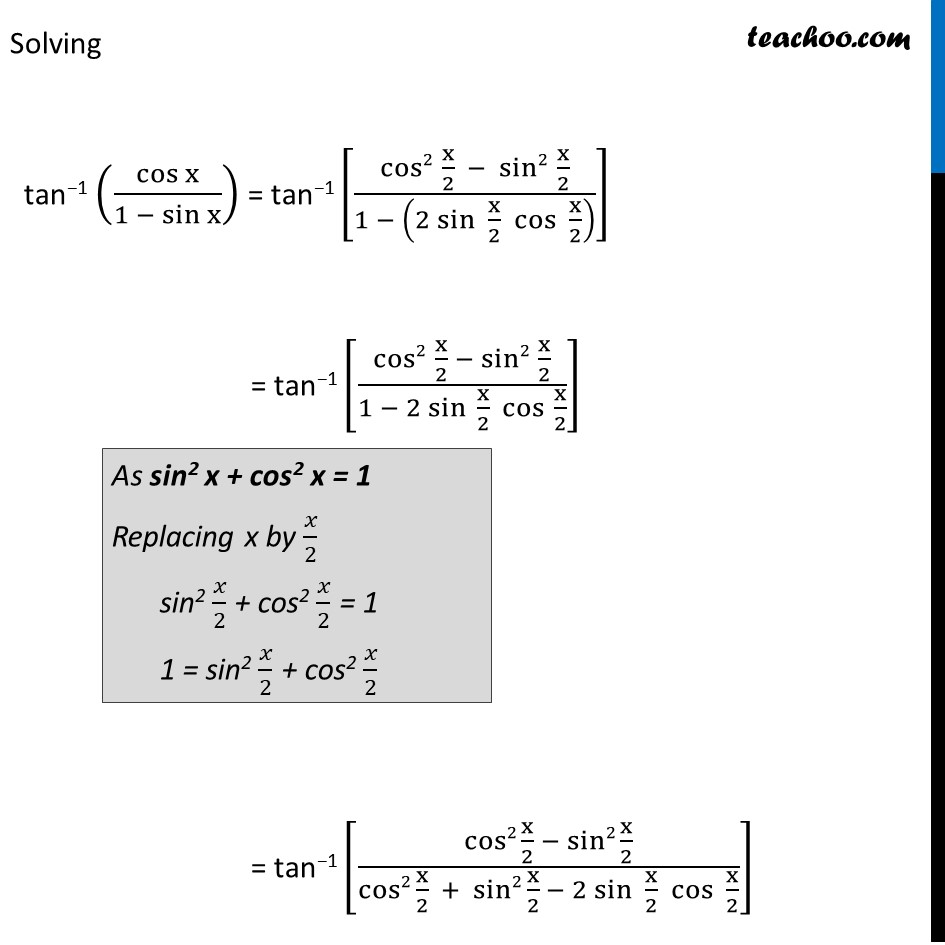
Example 4 Express tan−1 cos⁡x/(1 − sin⁡x ) , – π/2 < x < 3π/2 in the simplest form Lets first calculate cos x & 1 – sin x We know that cos 2x = 𝐜𝐨𝐬𝟐⁡𝐱 – 𝐬𝐢𝐧𝟐⁡𝐱 Replacing x by 𝑥/2 cos (2x/2) = cos2 x/2 – sin2 x/2 cos x = cos2 x/2 – sin2 x/2 We know that sin 2x = 2 sin x cos x Replacing x by 𝑥/2 sin (2𝑥/2) = 2 sin 𝑥/2 cos 𝑥/2 sin x = 2 sin 𝑥/2 cos 𝑥/2 Solving tan−1 (cos⁡x/(1 〖− sin〗⁡x )) = tan−1 [(cos2 x/2 − sin2 x/2)/(1 − (2 〖sin 〗⁡〖x/2 cos⁡〖 x/2〗 〗 ) )] = tan−1 [(cos2 x/2 − sin2 x/2)/(1 − 2 〖sin 〗⁡〖x/2 〖 cos 〗⁡〖x/2〗 〗 )] = tan−1 [(cos2 x/2 − sin2 x/2)/(cos2 x/2 + sin2 x/2 − 2 〖sin 〗⁡〖x/2 cos⁡〖 x/2〗 〗 )] As sin2 x + cos2 x = 1 Replacing x by 𝑥/2 sin2 𝑥/2 + cos2 𝑥/2 = 1 1 = sin2 𝑥/2 + cos2 𝑥/2 = tan−1 [(cos x/2 + sin x/2)(cos x/2 − sin x/2)/(cos x/2 − sin x/2)^2 ] = tan−1 [((cos x/2 + sin x/2))/((cos x/2 − sin x/2) )] Dividing by cos 𝑥/2 = tan−1 ((cos⁡〖 𝑥/( 2 )〗/〖𝑐𝑜𝑠 〗⁡〖 𝑥/2〗 + sin⁡〖 𝑥/( 2 )〗/〖𝑐𝑜𝑠 〗⁡〖 𝑥/2〗 )/(𝑐𝑜𝑠⁡〖 𝑥/( 2 )〗/〖𝑐𝑜𝑠 〗⁡〖 𝑥/2〗 − 𝑠𝑖𝑛⁡〖 𝑥/( 2 )〗/〖𝑐𝑜𝑠 〗⁡〖 𝑥/2〗 )) = tan−1 [(1 + 〖tan 〗⁡〖𝑥/2〗)/(1 − tan⁡〖 𝑥/2〗 )] = tan−1 [(𝟏 + 〖tan 〗⁡〖𝑥/2〗)/(1 − 〖𝟏 .tan〗⁡〖 𝑥/2〗 )] = tan−1 ((𝒕𝒂𝒏⁡〖 𝝅/𝟒〗 + 〖𝑡𝑎𝑛 〗⁡〖𝑥/2〗)/( 1− 〖𝒕𝒂𝒏 〗⁡〖𝝅/𝟒 〗.〖 𝑡𝑎𝑛 〗⁡〖𝑥/2〗 )) = tan−1 [tan⁡(π/4+x/2 ) ] = 𝛑/𝟒+𝐱/𝟐