Misc 9 - Chapter 14 Class 11 Probability

Transcript

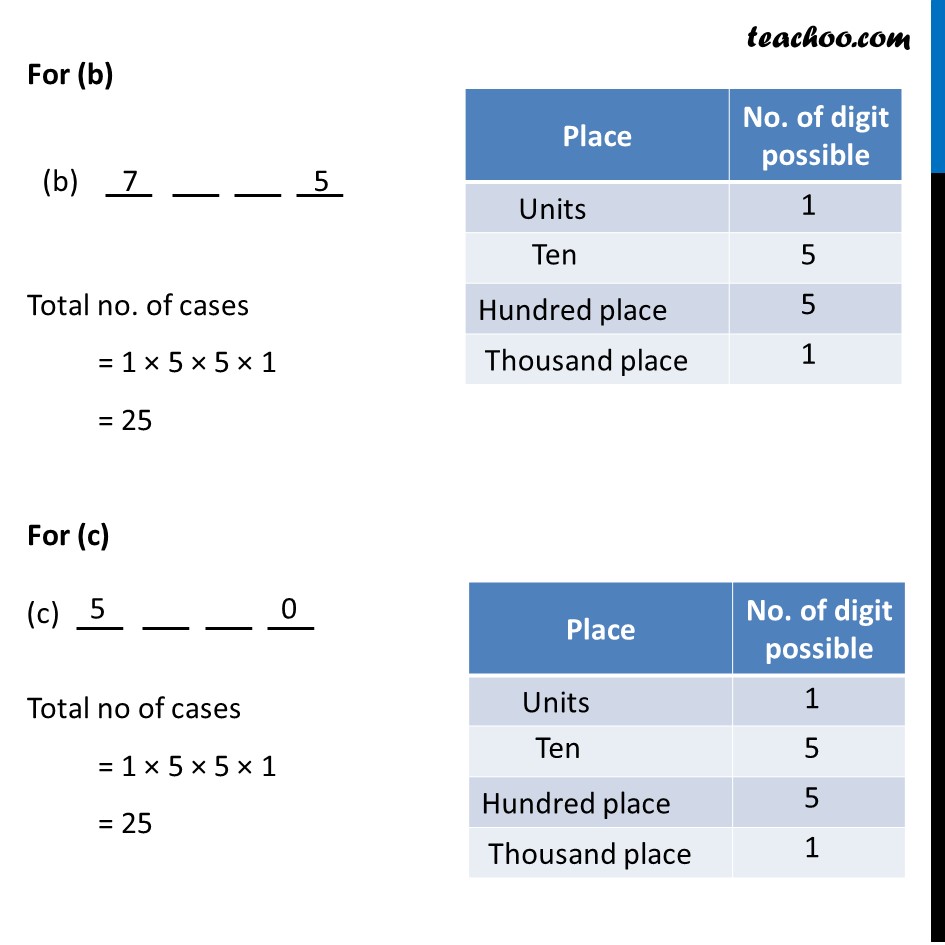
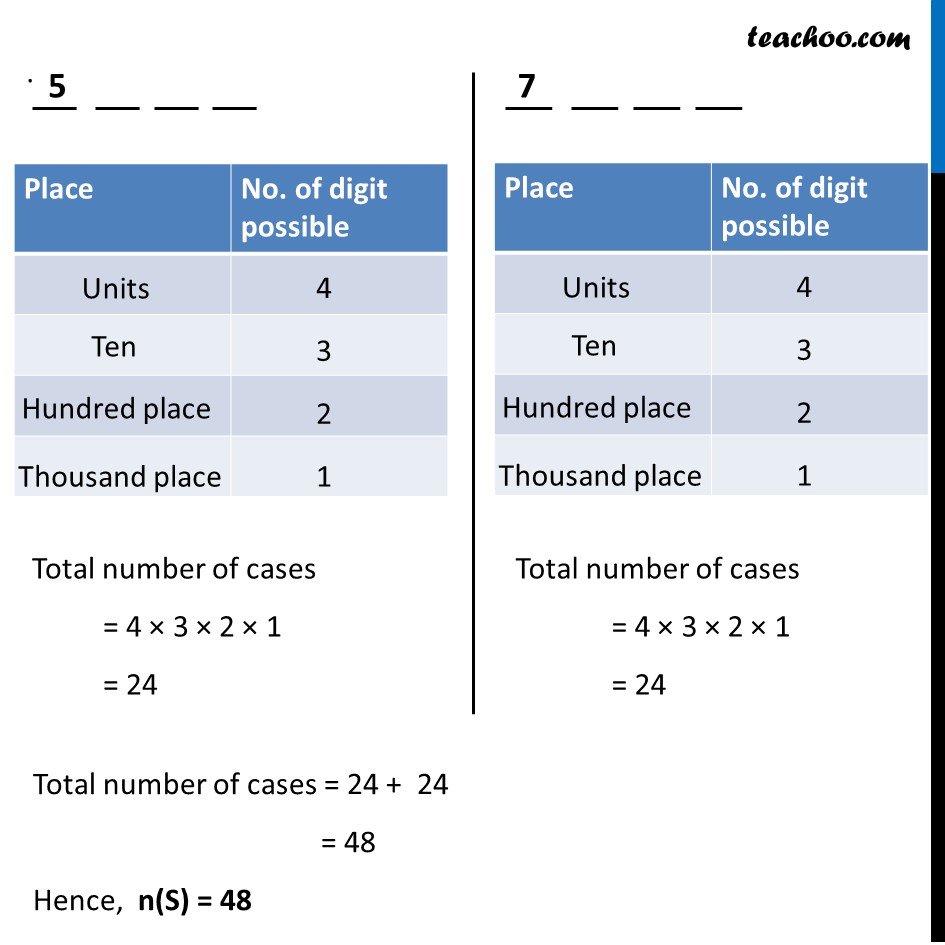
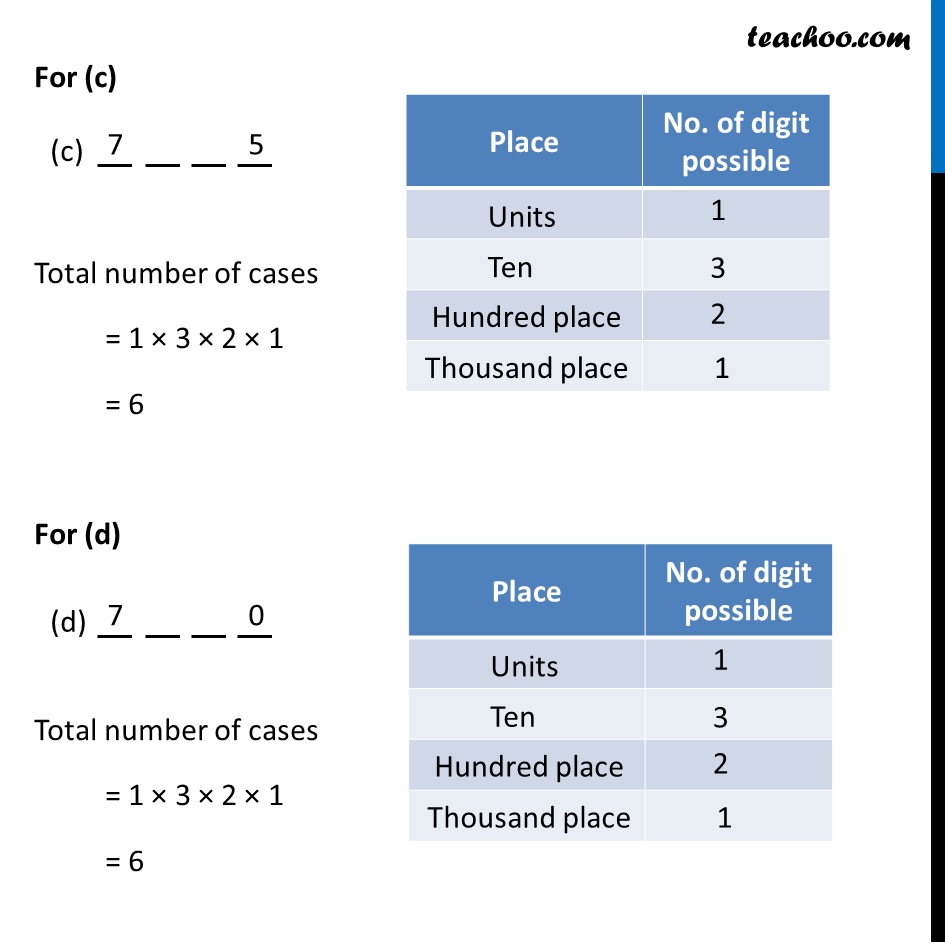
Misc 9 If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, (i) the digits are repeated? Digit number greater than 5000 can be formed with either 5 in beginning or 7 in beginning Hence total number of cases = 5 × 5 × 5 × 1 = 125 Hence total number of cases = 5 × 5 × 5 × 1 = 125 Total number of cases = 125 + 125 = 250 But if we get all 0’s after 5, we will get 5000. But we want number greater than 5000 Hence, n(S) = 250 – 1 = 249 Let A be the event that this number is divisible by 5 A number is divisible by 5 in the following cases For (a) Total no of cases = 1 × 5 × 5 × 1 = 25 5 at the end of number place 0 at the end of number place For (b) Total no. of cases = 1 × 5 × 5 × 1 = 25 For (c) Total no of cases = 1 × 5 × 5 × 1 = 25 But if we get all 0’s after 5, we will get 5000. But we want number greater than 5000 Number of cases = 25 – 1 = 24 For(d) Total no. of cases = 1 × 5 × 5 × 1 = 25 Hence, Total numbers divisible by 5 = 25 + 25 + 24 + 25 = 99 So, n(A) = 99 Hence, P(A) = (n(A))/(n(S)) = 99/249 = 𝟑𝟑/𝟖𝟑 Misc 9 If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, (ii) the repetition of digits is not allowed? Digit number greater than 5000 can be formed with either 5 in beginning or 7 in beginning Total number of cases = 4 × 3 × 2 × 1 = 24 Total number of cases = 4 × 3 × 2 × 1 = 24 Total number of cases = 24 + 24 = 48 Hence, n(S) = 48 Let B the event that the number greater than 5000 is divisible by 5 Hence it should have either 5 or 0 at unit place A number is divisible by 5 in the following cases For (b) Total number of cases = 1 × 3 × 2 × 1 = 6 Not possible as repetition is not allowed For (c) Total number of cases = 1 × 3 × 2 × 1 = 6 For (d) Total number of cases = 1 × 3 × 2 × 1 = 6 Hence Total number of cases when digit is divisible by 5 = 6 + 6 + 6 = 18 So, n(B) = 18 Hence, P(B) = (n(B))/(n(S)) = 18/48 = 𝟑/𝟖