Example 9 - Chapter 11 Class 11 - Intro to Three Dimensional Geometry

Transcript

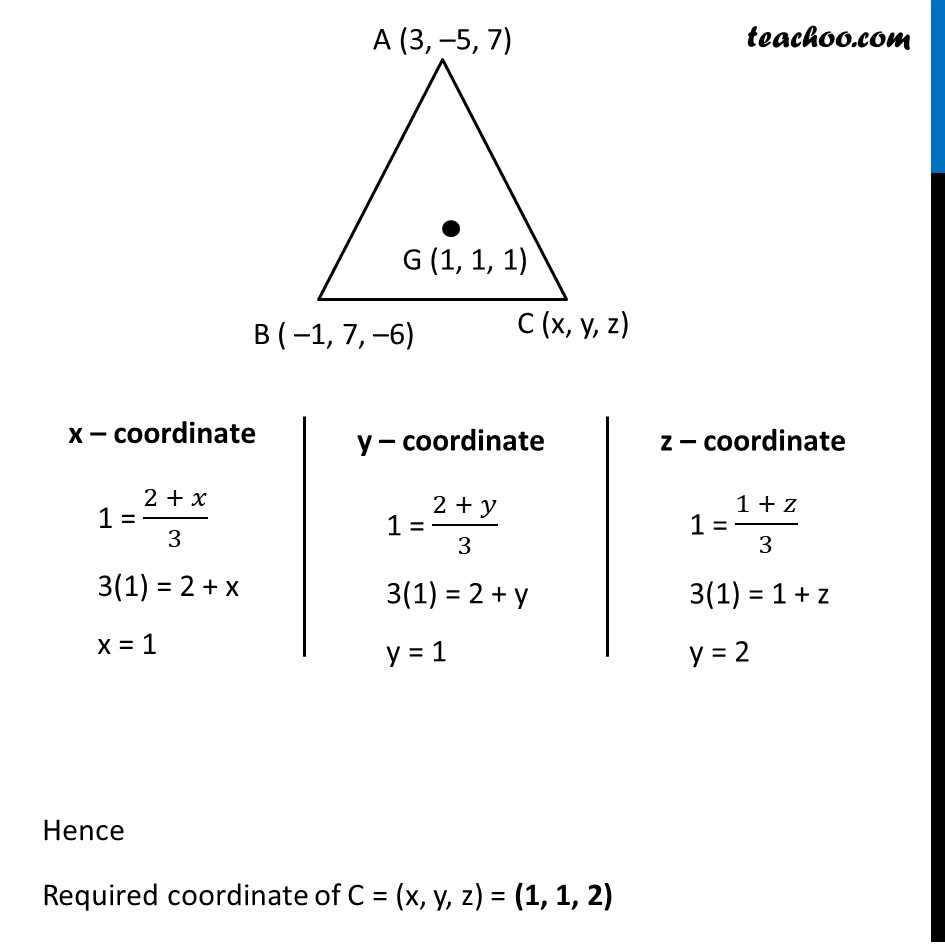
Example 9 The centroid of a triangle ABC is at the point (1, 1, 1). If the coordinates of A and B are (3, –5, 7) and (–1, 7, –6), respectively, find the coordinates of the point C. Let ABC be a triangle where A (3, –5, 7) , B( –1, 7, –6) Let G be the centroid of ∆ ABC So, G (1, 1, 1) Let Coordinate of C (x, y, z) We know that Co ordinate of centroid whose vertices are (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) is ((𝑥_1 + 𝑦_1 + 𝑧_1)/3,(𝑥_2 + 𝑦_2 + 𝑧_2)/3,(𝑥_3 + 𝑦_3 + 𝑧_3)/3) Here, x1 = 3 , y1 = –5 , z1 = 7 x2 = –1 , y2 = 7 , z2 = –6 x3 = x , y2 = y , z3 = z ∴ Coordinates of G (1, 1, 1) = ((3 + (−1) + 𝑥)/3,(−5 + 7 + 𝑦)/3,(7 + (−6) + 𝑧)/3) (1, 1, 1) = ((2 + 𝑥)/3,(2 + 𝑦)/3,(1 + 𝑧)/3) x – coordinate 1 = (2 + 𝑥)/3 3(1) = 2 + x x = 1 y – coordinate 1 = (2 + 𝑦)/3 3(1) = 2 + y y = 1 z – coordinate 1 = (1 + 𝑧)/3 3(1) = 1 + z y = 2 Hence Required coordinate of C = (x, y, z) = (1, 1, 2)