

Miscellaneous
Last updated at Dec. 16, 2024 by Teachoo



Transcript
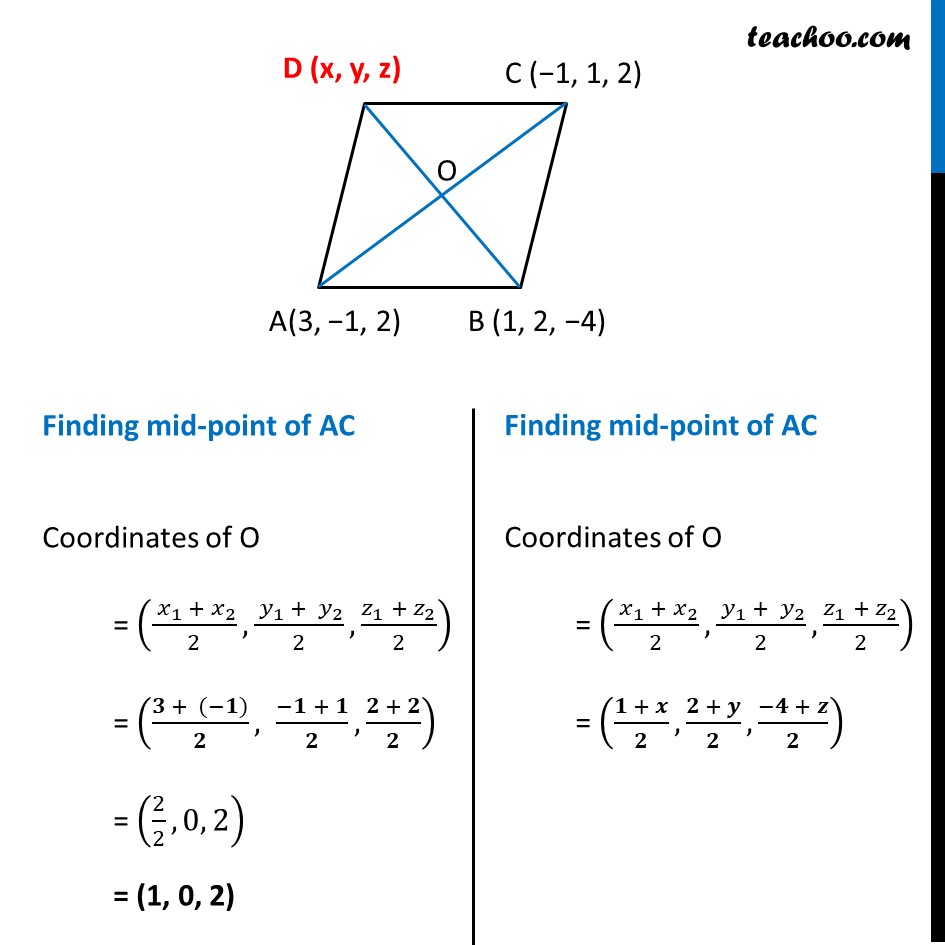
Misc 1 Three vertices of a parallelogram ABCD are A (3, –1, 2), B (1, 2, –4) and C (–1, 1, 2). Find the coordinates of the fourth vertex. In parallelogram, diagonals bisect each other Hence AO = OC & BO = OD We can say that O is Midpoint of AC and O is Midpoint of BD Finding co-ordinates of O Now, O is the mid-point of AC Here, A (3, –1. 2 ) & C ( –1 , 1, 2) We know that If O (x, y, z) is the mid point of A (x1, y1, z1) & B (x2, y2, z2) , then coordinates of O O (x, y, z) = ((〖 𝑥〗_1 +〖 𝑥〗_2)/2,(〖 𝑦〗_1 + 〖 𝑦〗_2)/2,(𝑧_1 +〖 𝑧〗_2)/2) Here, x1 = 3, y1 = –1, z1 = 2 x2 = –1 , y2 = 1, z2 = 2 Putting values, O = ((3 + (−1))/2, (−1 + 1)/2, (2 + 2)/2) = ((3 − 1)/2, 0/2, 4/2) = (2/2, 0, 2) = (1, 0, 2) Thus, the co-ordinates of O is (1, 0, 2) Now, O is also the mid-point of BD , Finding coordinates of O, Here, B (1, 2, –4) , O (1, 0, 2) Let D Be (x, y, z) Now Co-ordinates of O = ((1 + 𝑥)/2,(2 + 𝑦)/2, (−4 + 𝑧)/2) (1, 0, 2) = ((1 + 𝑥)/2, (2 + 𝑦)/2, (−4 + 𝑧)/2) Thus, x = 1 , y = -2 , z = 8 ∴ Coordinates of point D are (1, –2, 8) Thus, Coordinates of the fourth vertex are (1, –2, 8) (1 + 𝑥)/2=1 1 + x = 2 x = 2 – 1 x = 1 (2 + 𝑦)/2=0 2 + y = 0 × 2 2 + y = 0 y = – 2 (−4 + 𝑧)/2=2 – 4 + z = 2 × 2 z = 4 + 4 z = 8