Example 4 - Chapter 11 Class 11 - Intro to Three Dimensional Geometry

Transcript

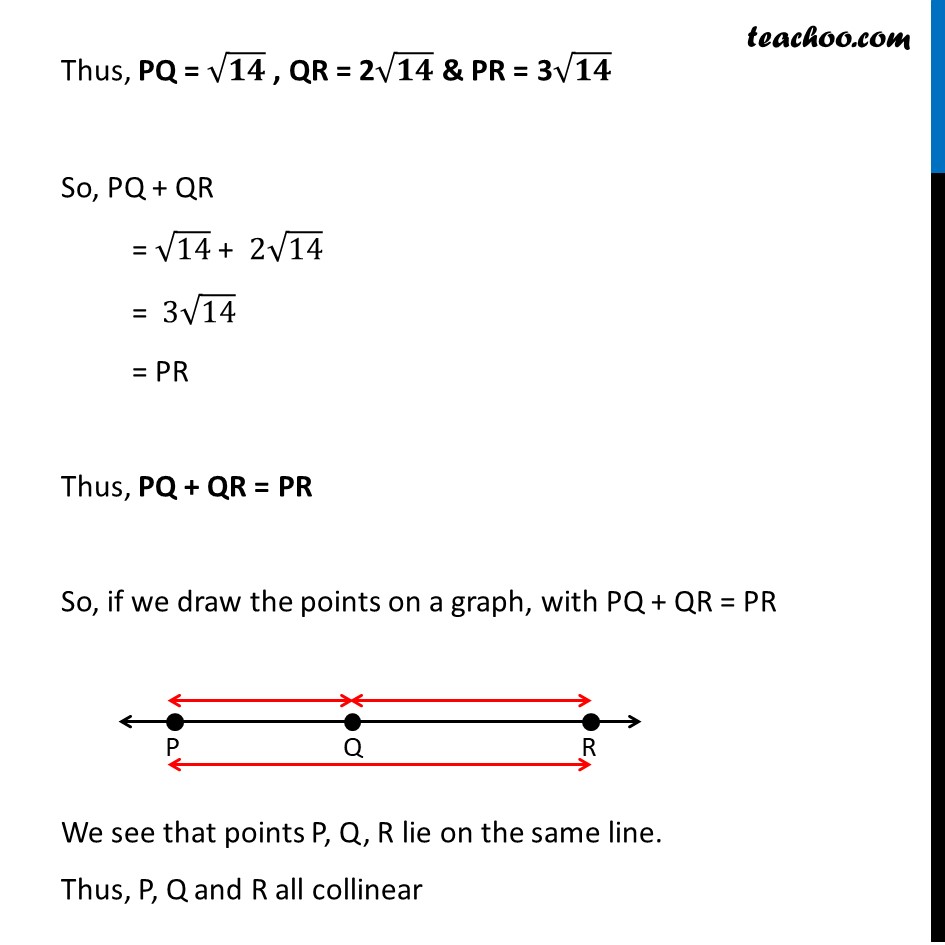
Example 4 Show that the points P (–2, 3, 5), Q (1, 2, 3) and R (7, 0, –1) are collinear. If three points are collinear, then they lie on a line. Let first calculate distance between the 3 points i.e. PQ. QR and PR Calculating PQ P ( – 2, 3, 5) Q (1, 2, 3) Hence , PQ = √((𝑥2−𝑥1)2+(𝑦2−𝑦1)2+(𝑧2 −𝑧1)2) PQ = √((1−(−2))2+(2−3)2+(3−5)2) = √((1+2)2+(2−3)2+(3−5)2) = √(32+(−1)2+(−2)2) = √(9+(−1)2+(−2)2) = √(9+1+4) = √𝟏𝟒 Calculating QR Q ( 1, 2, 3) R (7, 0, –1) QR = √((x2−x1)2+(y2−y1)2+(z2 −z1)2) Here , x1 = – 2, y1 = 3, z1 = 5 x2 = 1, y2 = 2, z2 = 3 QR = √((7−1)2+(0−2)2+(−1−3)2) = √((6)2+(−2)2+(−4)2) = √(36+4+16) = √56 = √(14 × 2 × 2) = 2√𝟏𝟒 Calculating PR P (–2, 3, 5), R (7, 0, –1) PR = √((x2−x1)2+(y2−y1)2+(z2 −z1)2) Here, x1 = –2, y1 = 3, z1 = 5 x2 = 7, y2 = 0, z2 = – 1 PR = √((7−(−2))2+(0−3)2+(−1−5)2) = √((7+2)2+(−3)2+(−6)2) = √((9)2+9+36) = √(81+9+36) = √126 = √(14 × 3 × 3) = 𝟑√𝟏𝟒 Thus, PQ = √𝟏𝟒 , QR = 2√𝟏𝟒 & PR = 3√𝟏𝟒 So, PQ + QR = √14 + 2√14 = 3√14 = PR Thus, PQ + QR = PR So, if we draw the points on a graph, with PQ + QR = PR We see that points P, Q, R lie on the same line. Thus, P, Q and R all collinear