Check sibling questions

Question 5 - Converting one shape to another - Chapter 12 Class 10 Surface Areas and Volumes

Last updated at May 29, 2023 by

Ex 13.3, 5 - A container shaped like a cylinder diameter 12 cm - Ex 13.3

Ex 13.3, 5 - Chapter 13 Class 10 Surface Areas and Volumes - Part 2
Ex 13.3, 5 - Chapter 13 Class 10 Surface Areas and Volumes - Part 3 Ex 13.3, 5 - Chapter 13 Class 10 Surface Areas and Volumes - Part 4

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

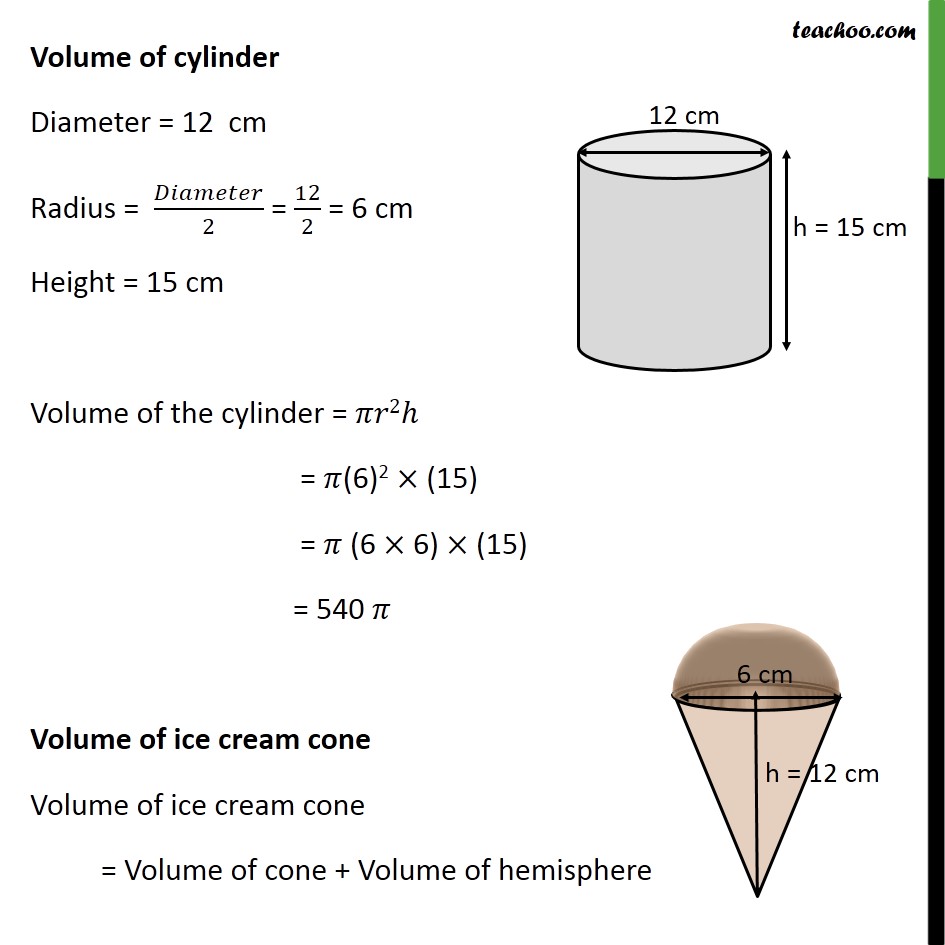
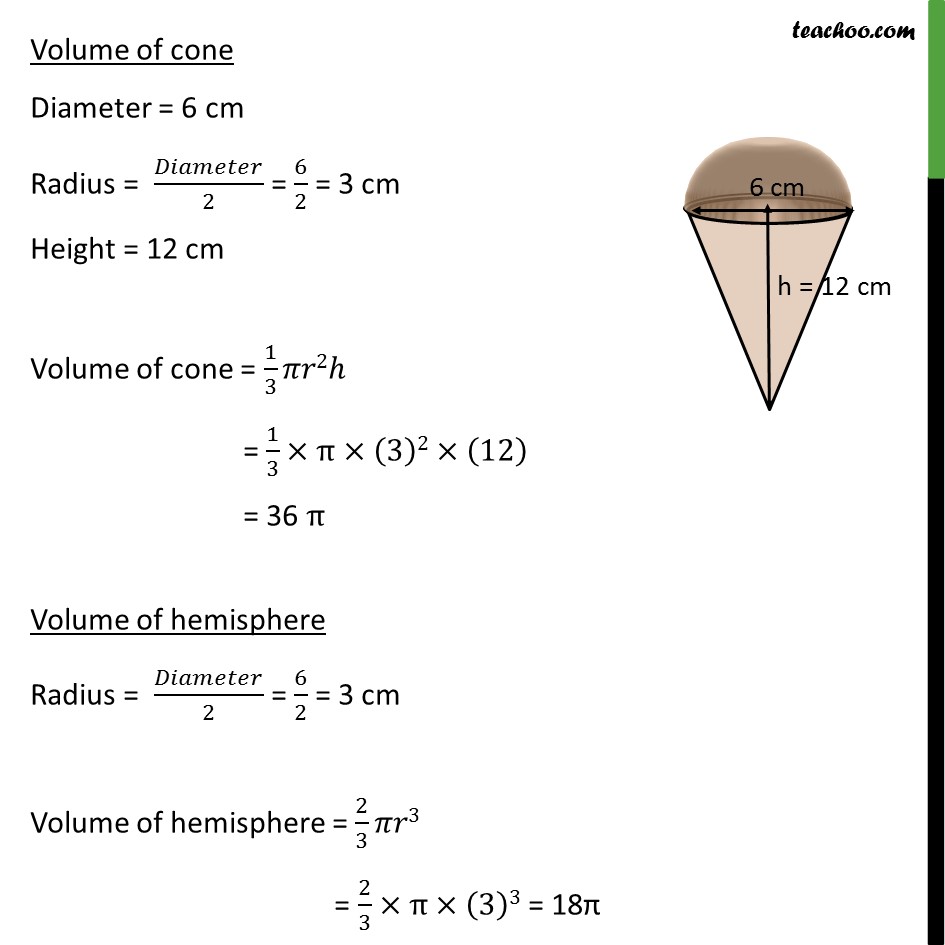
Question 5 A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream. Number of cones = ( )/( ) Volume of cylinder Diameter = 12 cm Radius = /2 = 12/2 = 6 cm Height = 15 cm Volume of the cylinder = 2 = (6)2 (15) = (6 6) (15) = 540 Volume of ice cream cone Volume of ice cream cone = Volume of cone + Volume of hemisphere Volume of cone Diameter = 6 cm Radius = /2 = 6/2 = 3 cm Height = 12 cm Volume of cone = 1/3 2 = 1/3 (3)2 (12) = 36 Volume of hemisphere Radius = /2 = 6/2 = 3 cm Volume of hemisphere = 2/3 3 = 2/3 (3)3 = 18 Hence, Volume of ice cream cone = Volume of cone + Volume of hemisphere = 36 + 18 = 54 Now, Number of cones = ( )/( ) = 540 /54 = 10 So, number of cones is 10.

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.