Ex 12.1, 8 - Chapter 12 Class 10 Surface Areas and Volumes

Transcript

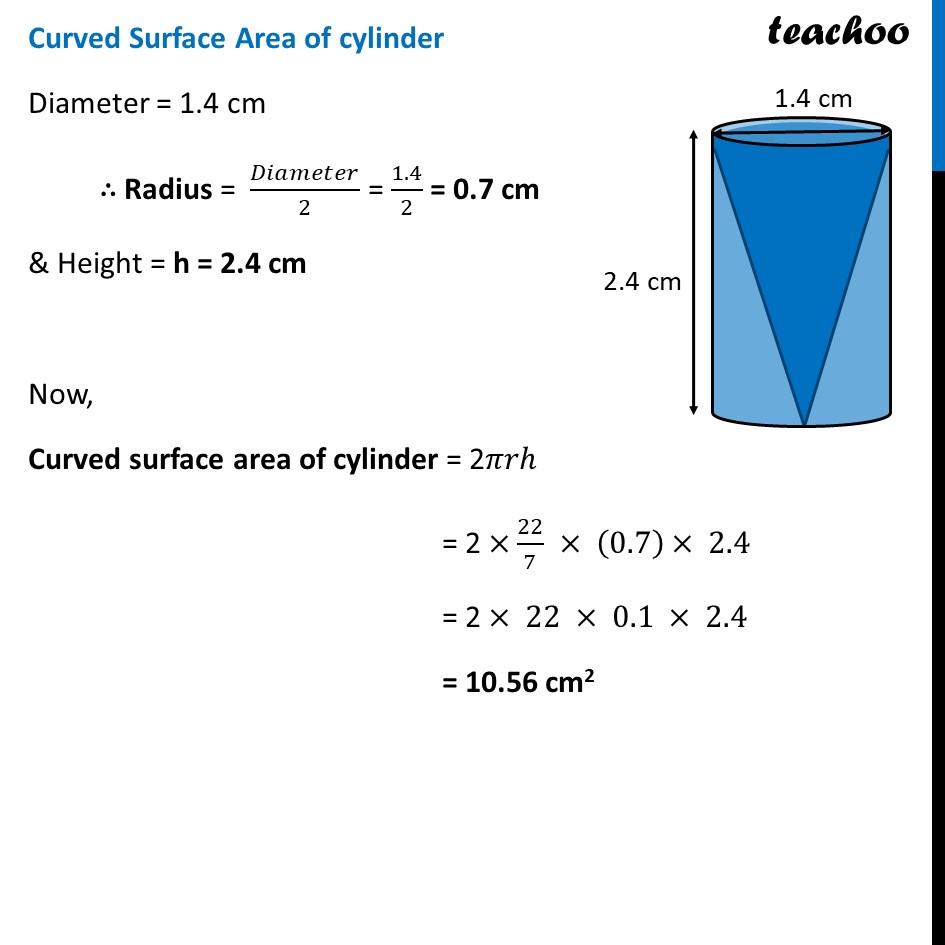
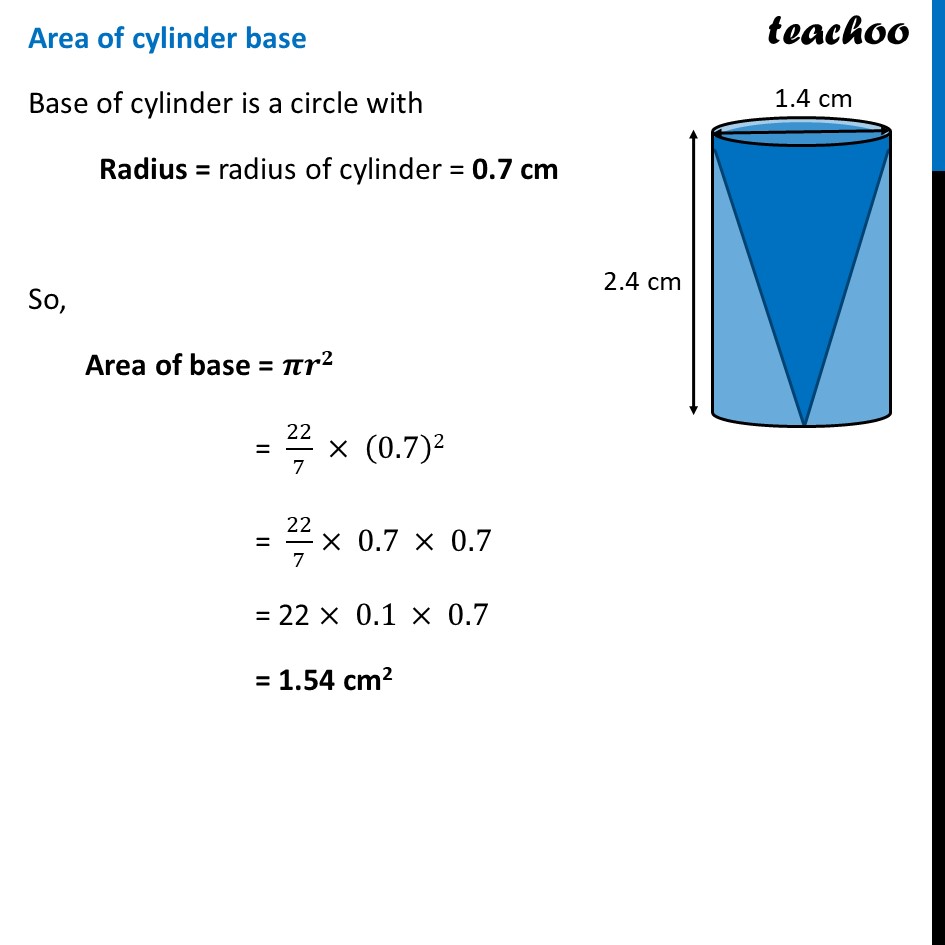
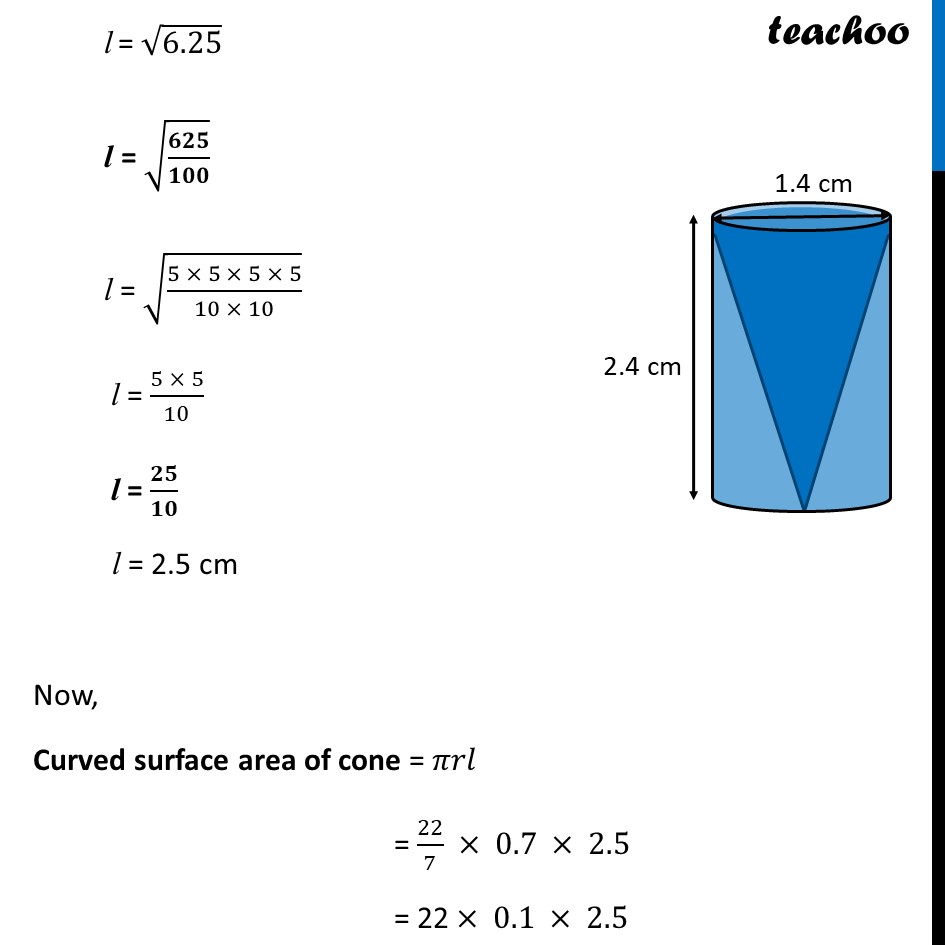
Ex 12.1,8 From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2. Since cylinder is solid, it has a base also whose area is also to be calculated. Now, Total surface area of remaining solid = Curved Surface Area of cylinder + Area of cylinder base + Curved surface area of cone Curved Surface Area of cylinder Diameter = 1.4 cm ∴ Radius = 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟/2 = 1.4/2 = 0.7 cm & Height = h = 2.4 cm Now, Curved surface area of cylinder = 2𝜋𝑟ℎ = 2 ×22/7 × (0.7)× 2.4 = 2 × 22 × 0.1 × 2.4 = 10.56 cm2 Area of cylinder base Base of cylinder is a circle with Radius = radius of cylinder = 0.7 cm So, Area of base = 𝝅𝒓𝟐 = 22/7 × (0.7)2 = 22/7× 0.7 × 0.7 = 22 × 0.1 × 0.7 = 1.54 cm2 Curved Surface area of cone Curved Surface area of cone = 𝝅𝒓𝒍 Now, Radius of cone = Radius of cylinder = 0.7 cm Height of cone = h = 2.4 cm Now, we find slant height (l) We know that l2 = h2 + r2 l2 = (2.4)2 + (0.7)2 l2 = (2.4 × 2.4 )2 + (0.7 × 0.7)2 l2 = 5.76 + 0.49 l2 = 6.25 l = √6.25 l = √(𝟔𝟐𝟓/𝟏𝟎𝟎) l = √((5 × 5 × 5 × 5)/(10 × 10)) l = (5 × 5)/10 l = 𝟐𝟓/𝟏𝟎 l = 2.5 cm Now, Curved surface area of cone = 𝜋𝑟𝑙 = 22/7 × 0.7 × 2.5 = 22 × 0.1 × 2.5 = 5.5 cm2 Hence, Total surface area of remaining solid = Curved Surface Area of cylinder + Area of cylinder base + curved surface area of cone = 10.56 + 1.54 + 5.5 = 17.6 cm2 Hence, area of remaining solid surface = 17.6 cm2 = 18 cm2 (approximately)