Ex 13.1, 5 - Chapter 13 Class 10 Surface Areas and Volumes (Term 2)

Transcript

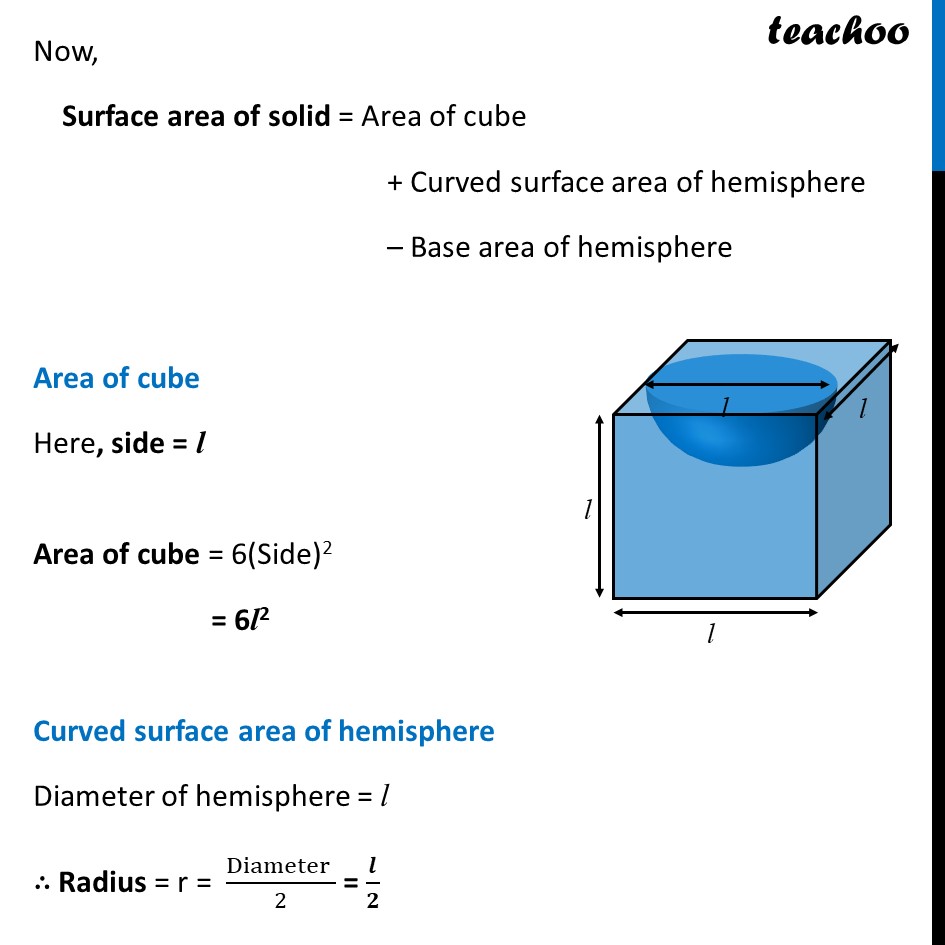
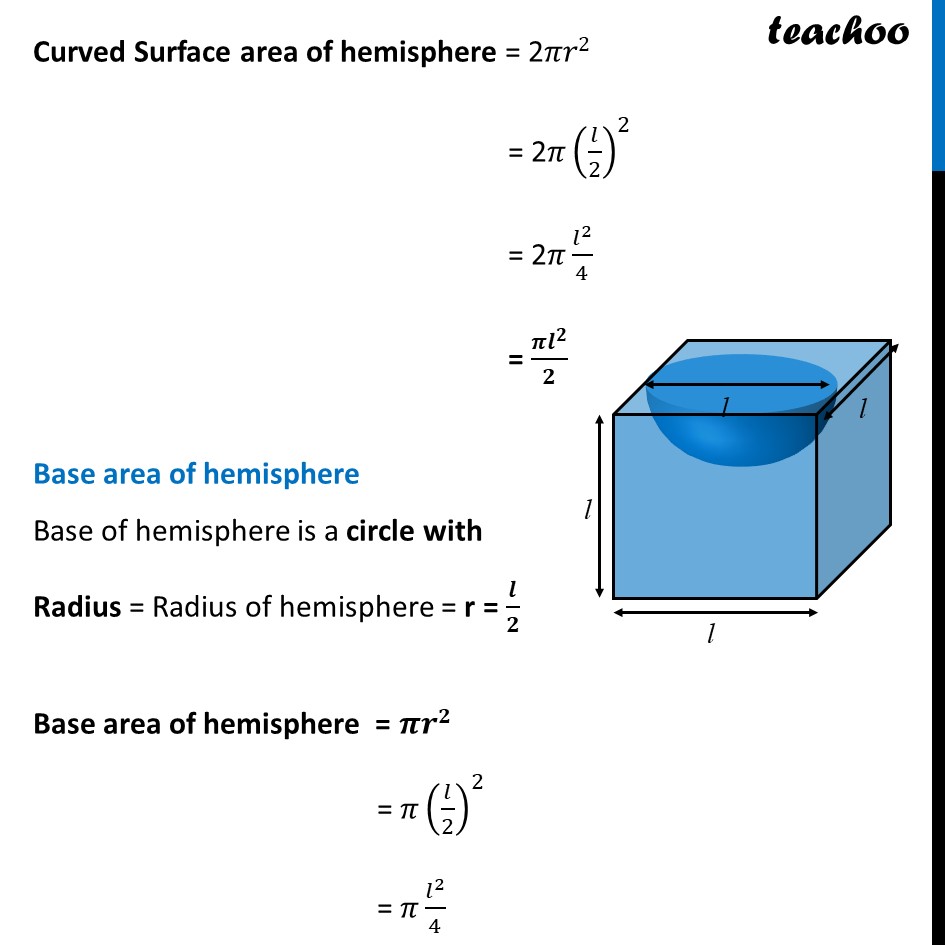
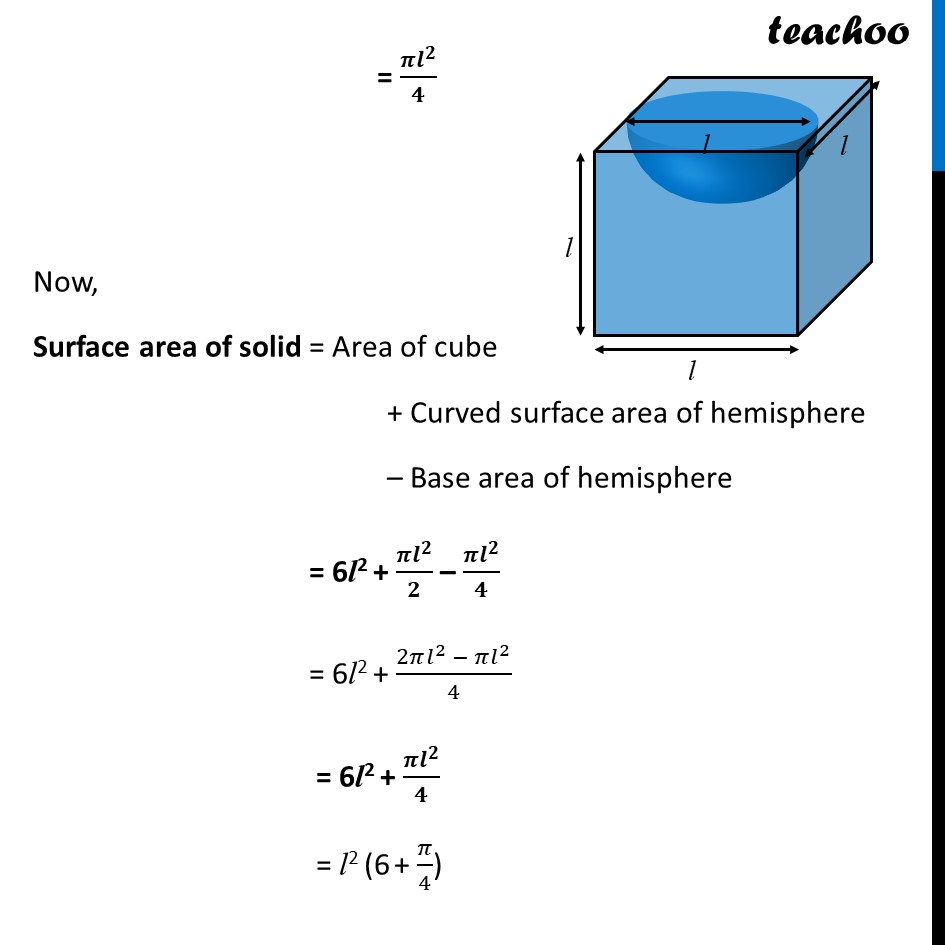
Ex 13.1, 5 A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid. Here, diameter of the hemisphere is equal to the edge of the cube So, diameter = side of cube = l Here, base of hemisphere would not be included in the total solid area of wooden cube . Surface area of solid = Area of cube + Curved surface area of hemisphere Base area of hemisphere Area of cube Here, side = l Area of cube = 6(Side)2 = 6l2 Curved surface area of hemisphere Diameter of hemisphere = l Hence, radius = r = (Diameter )/2 = /2 Curved Surface area of hemisphere = 2 2 = 2 ( /2)^2 =2 ^2/4 = ( ^2)/2 Base area of hemisphere Base of hemisphere is a circle with radius = radius of hemisphere = r = /2 Base area of hemisphere = 2 = ( /2)^2 = ^2/4 = ( ^2)/4 Now, Surface area of solid = Area of cube + Curved surface area of hemisphere Base area of hemisphere = 6l2 + ( ^2)/2 ( ^2)/4 = 6l2 + (2 ^2 ^2)/4 = 6l2 + ( ^2)/4 = l2 (6 + /4) = l2 ((6(4) + )/4) = l2 ((24 + )/4) = 1/4l2 ( + 24) Hence, Surface area of solid = 1/4l2 ( + 24)