Ex 12.2, 13 - Chapter 12 Class 10 Areas related to Circles (Term 1)

Transcript

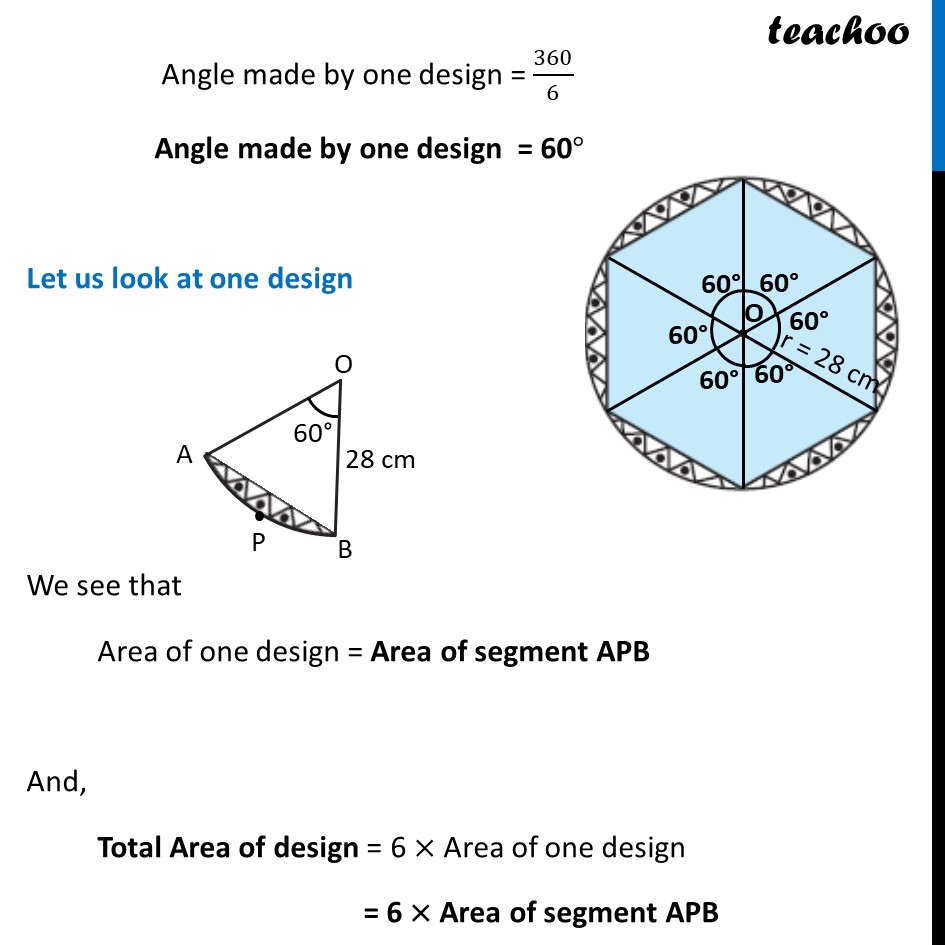
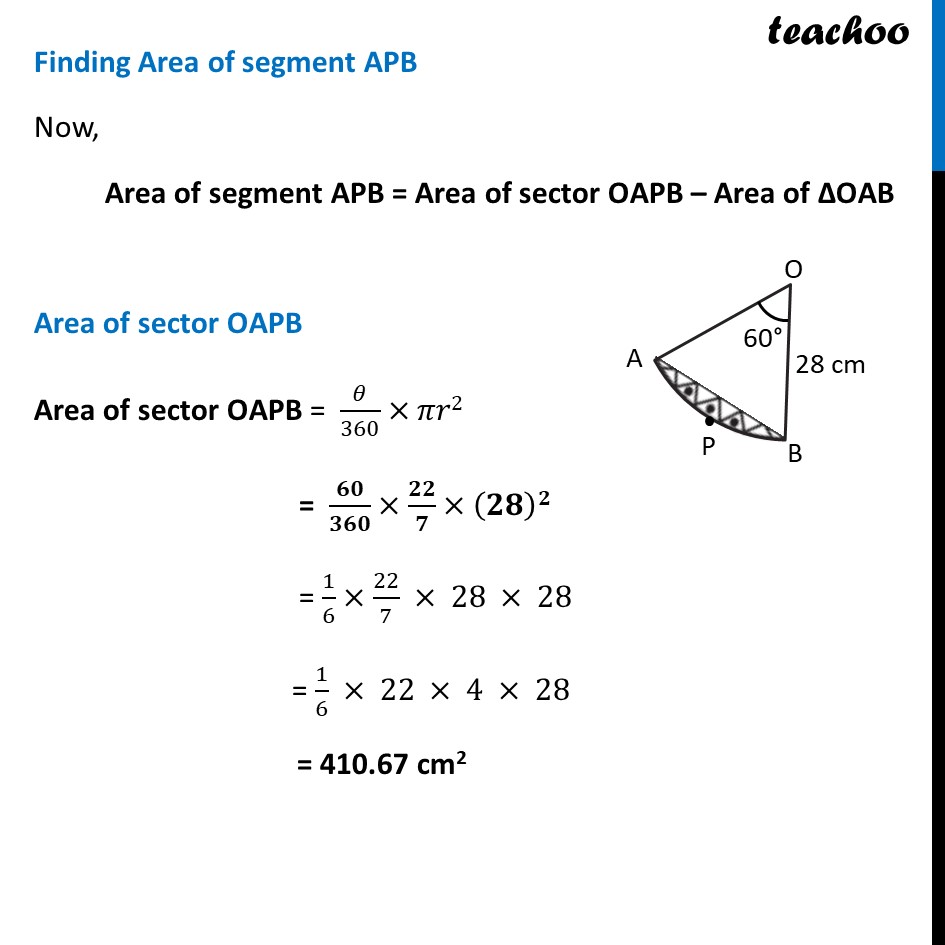
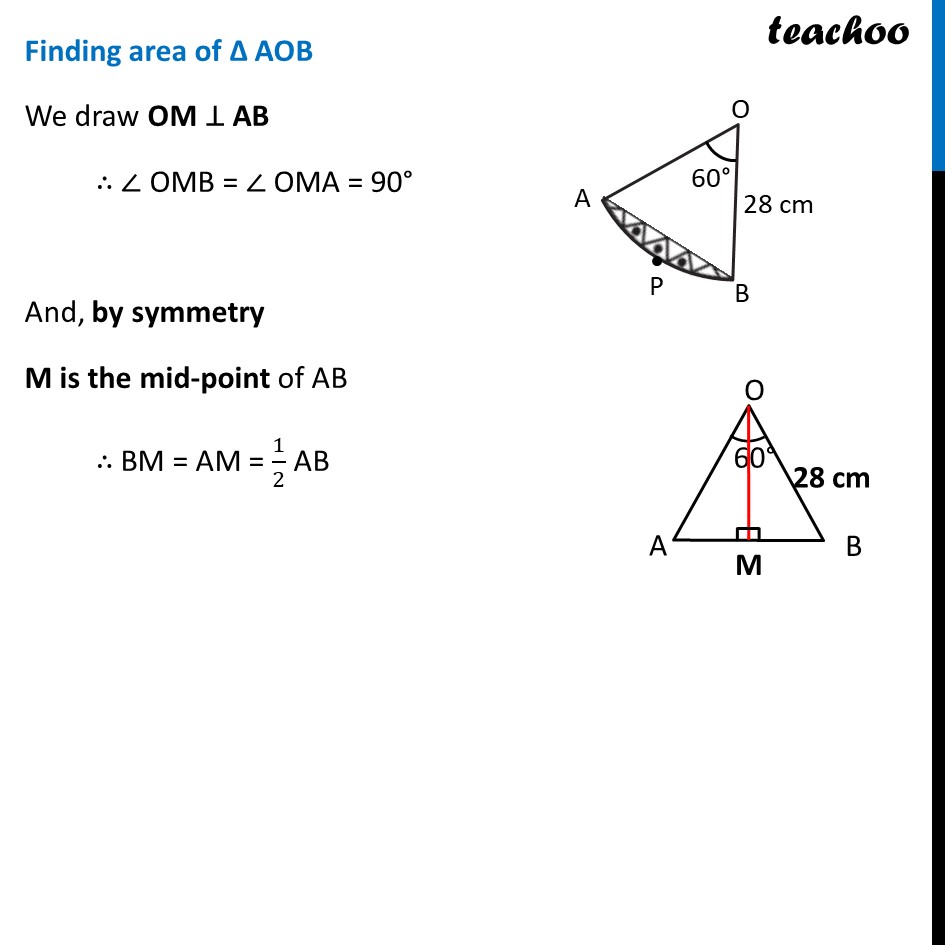
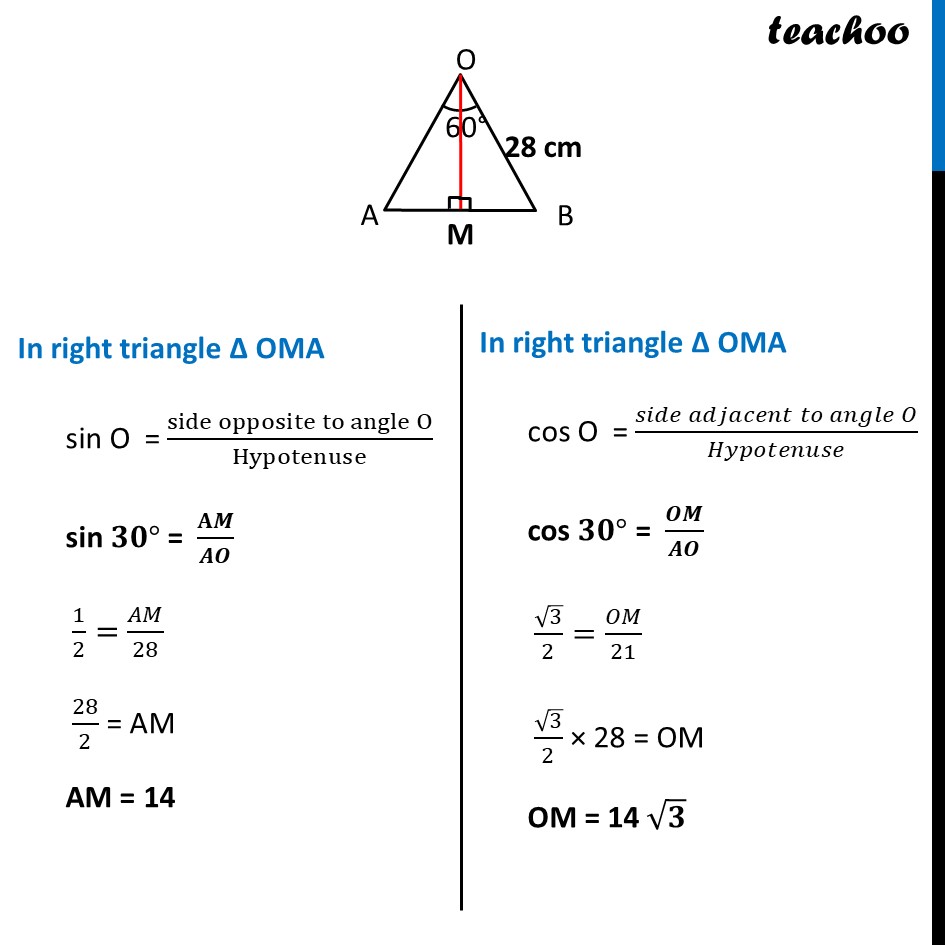
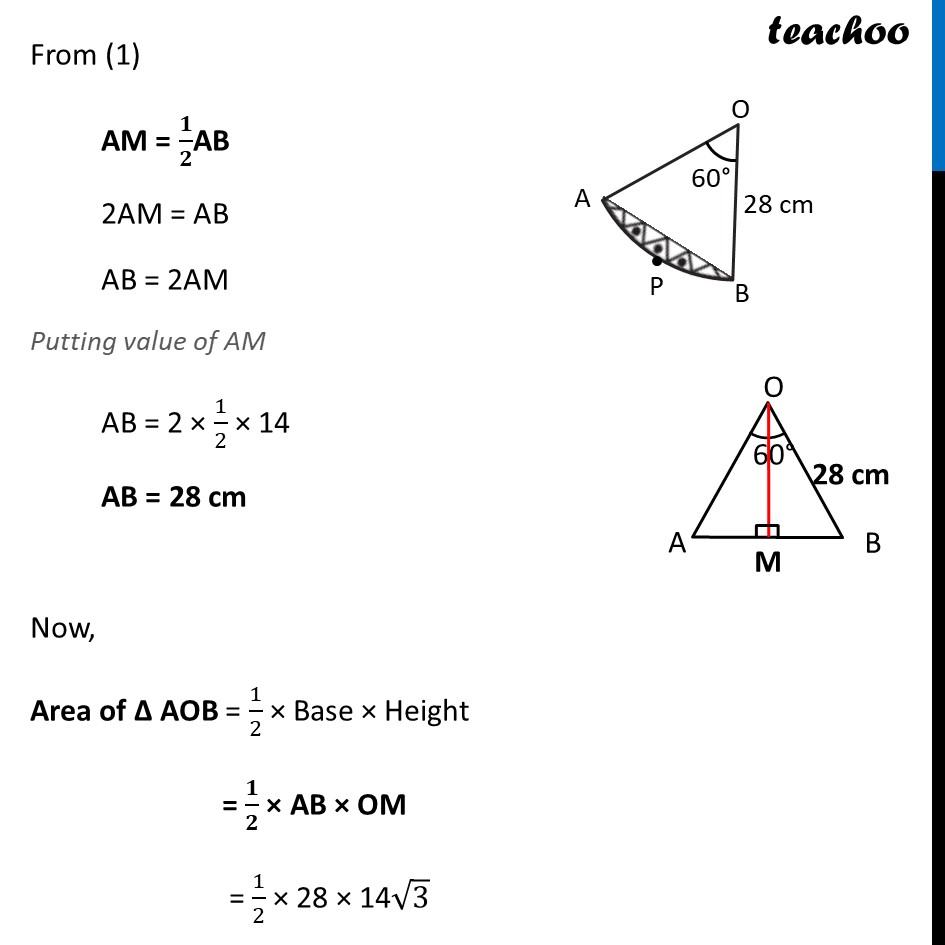
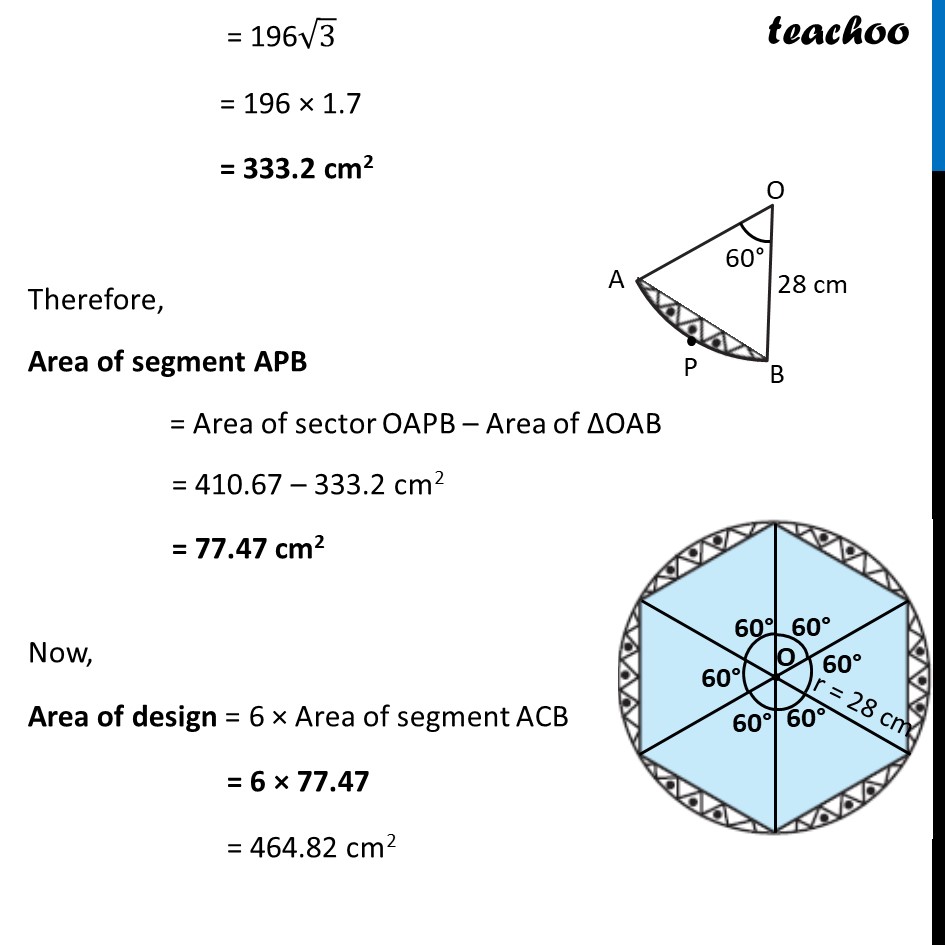
Ex 12.2, 13 A round table cover has six equal designs as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2. (Use 3 = 1.7) In the question a round table cover is given which has six equal designs. Let us join ends of the design Since the designs are equal, the angle made by the designs at point O will be equal. We know that sum of angles at a point = 360 6 Angle made by one design = 360 Angle made by one design = 360/6 Angle made by one design = 60 Let us look at one design We see that Area of one design = Area of segment APB & Total Area of design = 6 Area of one design = 6 Area of segment APB Area of segment APB = Area of sector OAPB Area of OAB Area of sector OAPB = /360 2 = 60/360 22/7 (28)2 = 1/6 22/7 28 28 = 1/6 22 4 28 = 410.67 cm2 Finding area of AOB Area AOB = 1/2 Base Height We draw OM AB OMB = OMA = 90 In OMA & OMB OMA = OMB OA = OB OM = OM OMA OMB AOM = BOM AOM = BOM = 1/2 BOA AOM = BOM = 1/2 60 = 30 Also, since OMB OMA BM = AM BM = AM = 1/2 AB From (1) AM = 1/2AB 2AM = AB AB = 2AM Putting value of AM AB = 2 14 AB = 28 Now, Area of AOB = 1/2 Base Height = 1/2 AB OM = 1/2 28 14 3 = 196 3 = 196 1.7 = 333.2 cm2 Area of the segment APB = Area of sector OAPB Area of AOB = 410.67 333.2 cm2 = 77.47 cm2 Now Area of design = 6 Area of segment ACB = 6 77.47 = 464.82 cm2 Cost of making 1 cm2 design = Rs 0.35 Cost of making 464.82 cm2 design = Rs 0.35 464.82 = Rs 162.68