EX 9.1, 8

Transcript

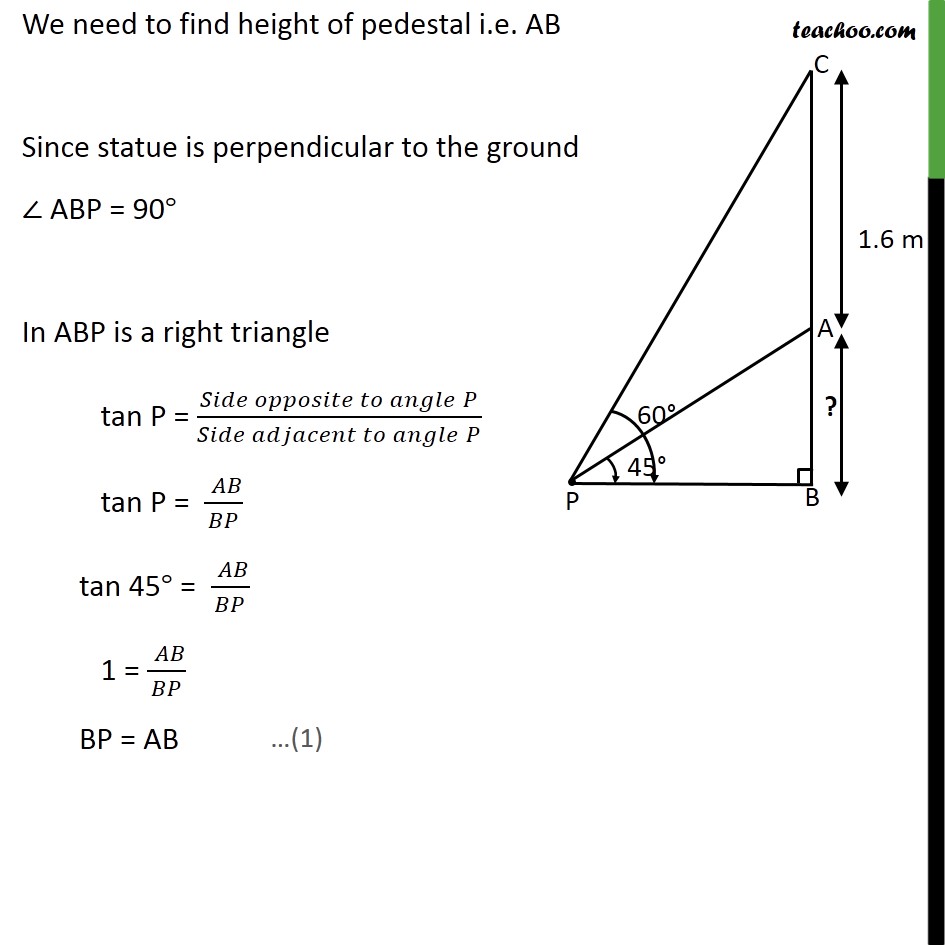
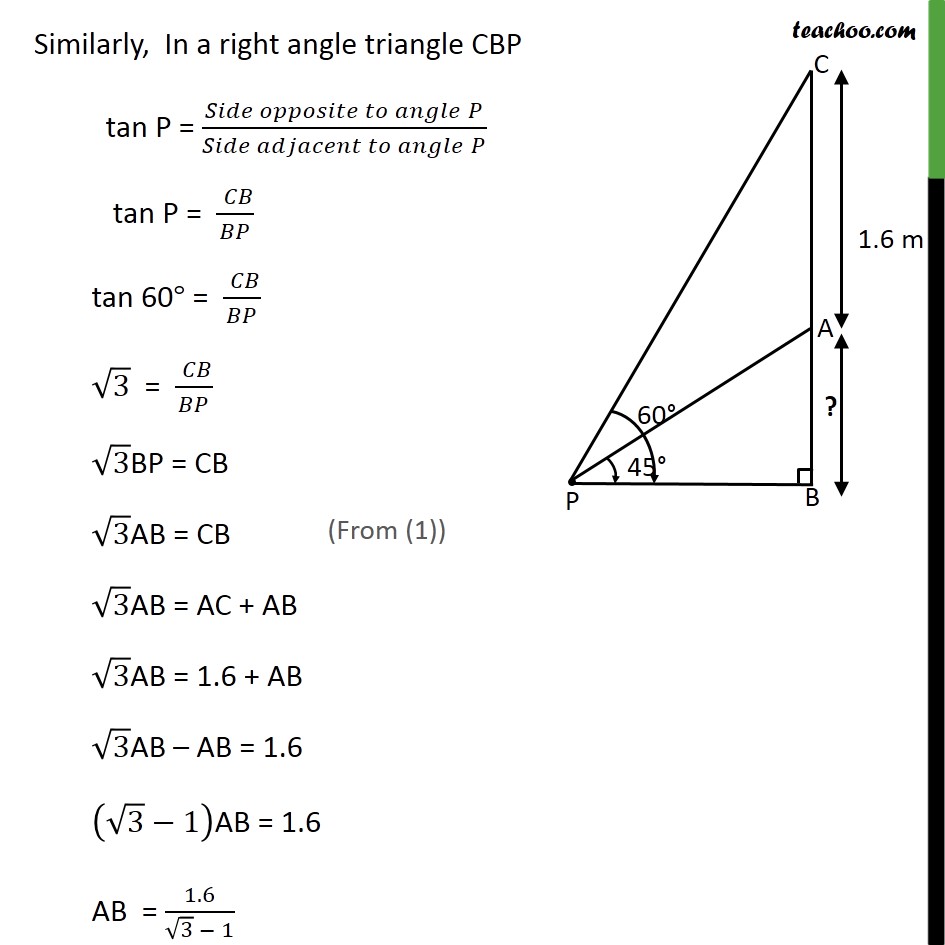
Ex 9.1 , 8 A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal. Here pedestal is AB & Statue is AC Height of pedestal = AB Length of the statue = 1.6m Hence, AC = 1.6m Angle of elevation to top of statue = 60° Hence, ∠CPB = 60° Angle of elevation at the top of the pedestal = 45° Hence, ∠APB = 45° We need to find height of pedestal i.e. AB Since statue is perpendicular to the ground ∠ ABP = 90° In ABP is a right triangle tan P = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃) tan P = (" " 𝐴𝐵)/𝐵𝑃 tan 45° = (" " 𝐴𝐵)/𝐵𝑃 1 = (" " 𝐴𝐵)/𝐵𝑃 BP = AB Similarly, In a right angle triangle CBP tan P = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃) tan P = (" " 𝐶𝐵)/𝐵𝑃 tan 60° = (" " 𝐶𝐵)/𝐵𝑃 √3 = (" " 𝐶𝐵)/𝐵𝑃 √3BP = CB √3AB = CB √3AB = AC + AB √3AB = 1.6 + AB √3AB – AB = 1.6 (√3−1)AB = 1.6 AB = 1.6/(√3 − 1)Rationalizing Multiplying (√3 " + 1)" in numerator and denominator AB = 1.6/(√3 − 1) × (√3 + 1)/(√3 + 1) AB = (1.6 × (√3 + 1))/((√3)^2 − 1^2 ) AB = (1.6 × (√3 + 1))/(3 −1) AB = (1.6 × (√3 + 1))/2 AB = 0.8 (√3 " + 1") Hence, Height of pedestal = AB = 0.8 (√3 " + 1") "m"