

Last updated at Dec. 13, 2024 by Teachoo




Transcript
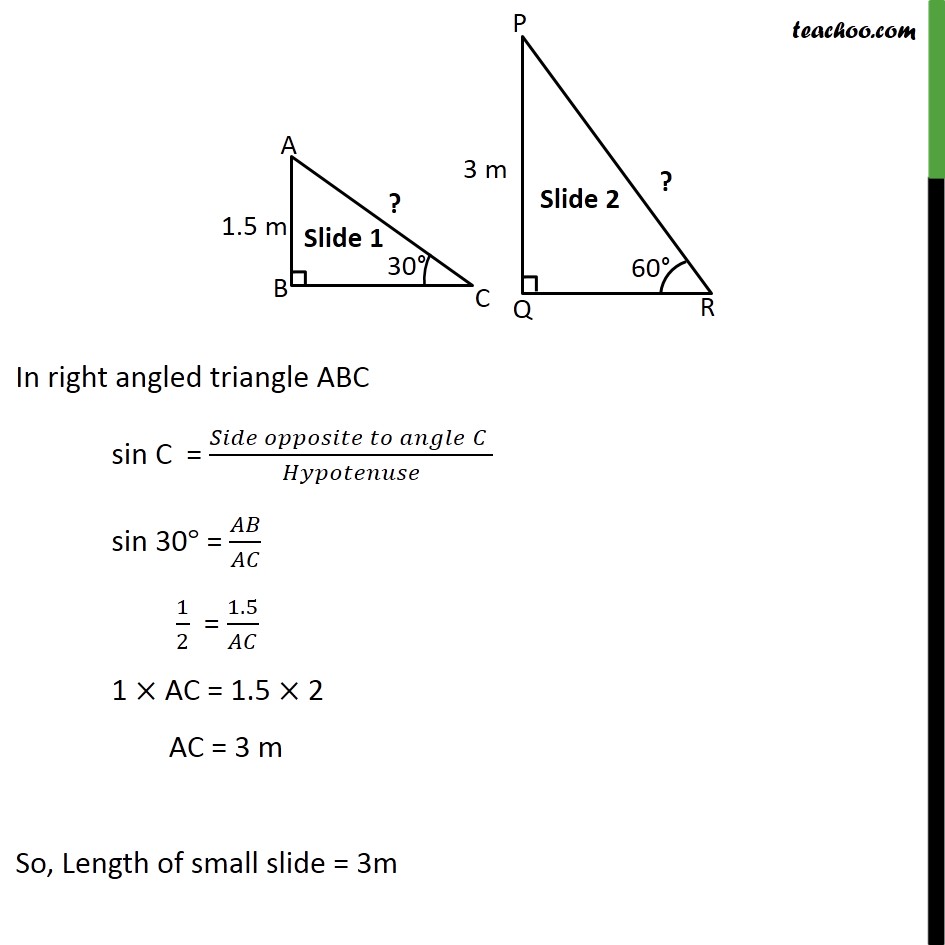
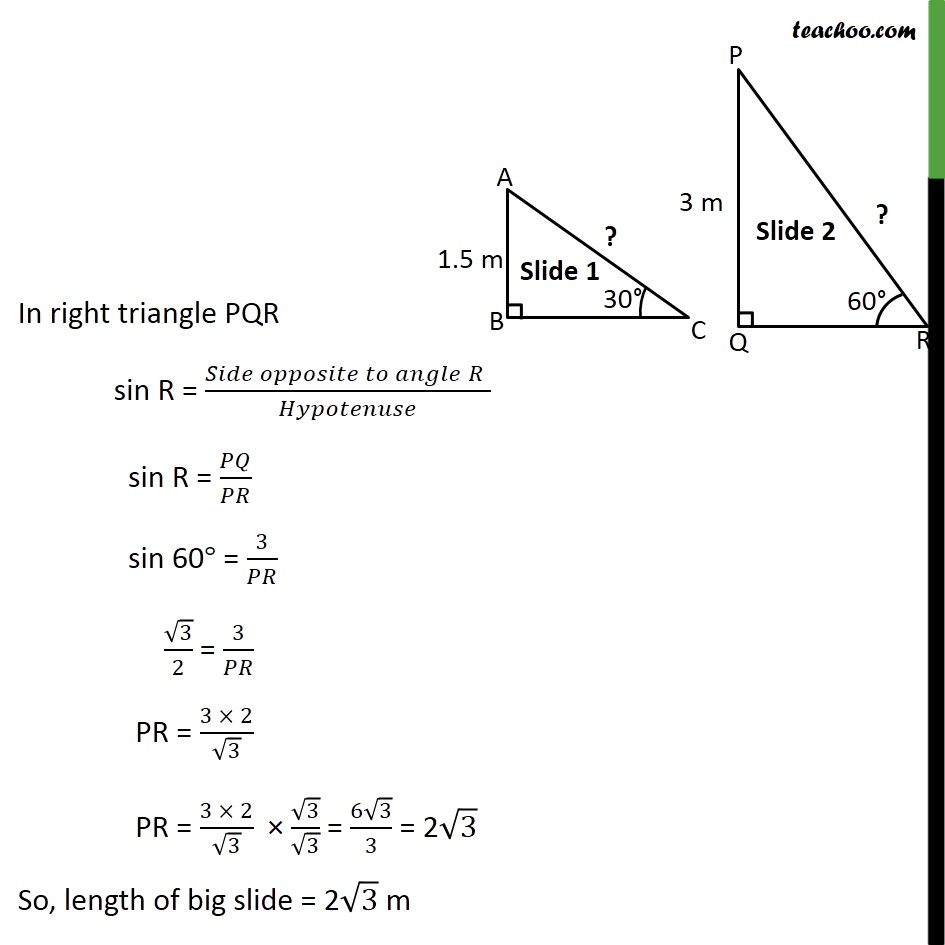
Ex 9.1 , 3 A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case? Let smaller slide be represented by right angle triangle ABC. Here, Height of small slide = 1.5m So, AB = 1.5m Also it is inclined at an angle of 30° to the ground. Hence, ∠ACB = 30° We need to find the length of slide i.e. AC. In right angled triangle ABC sin C = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐶" " )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 sin 30° = 𝐴𝐵/𝐴𝐶 1/2 = 1.5/𝐴𝐶 1 × AC = 1.5 × 2 AC = 3 m So, Length of small slide = 3m Similarly, we can do for larger slide Let larger slide be represented by right angle triangle PQR. Height of large slide = 3m So, PQ = 3m Also it is inclined at an angle of 60° to the ground. Hence, ∠PRQ = 60° We need to find the length of slide i.e. PR. In right triangle PQR sin R = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑅" " )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 sin R = 𝑃𝑄/𝑃𝑅 sin 60° = 3/𝑃𝑅 √3/2 = 3/𝑃𝑅 PR = (3 × 2)/√3 PR = (3 × 2)/√3 × √3/√3 = (6√3)/3 = 2√3 So, length of big slide = 2√3 m