Ex 9.1, 7 - Chapter 9 Class 10 Some Applications of Trigonometry

Last updated at April 16, 2024 by

Ex 9.1, 7 - From a point on ground, angles of elevation - Ex 9.1

Ex 9.1, 7 - Chapter 9 Class 10 Some Applications of Trigonometry - Part 2
Ex 9.1, 7 - Chapter 9 Class 10 Some Applications of Trigonometry - Part 3

Transcript

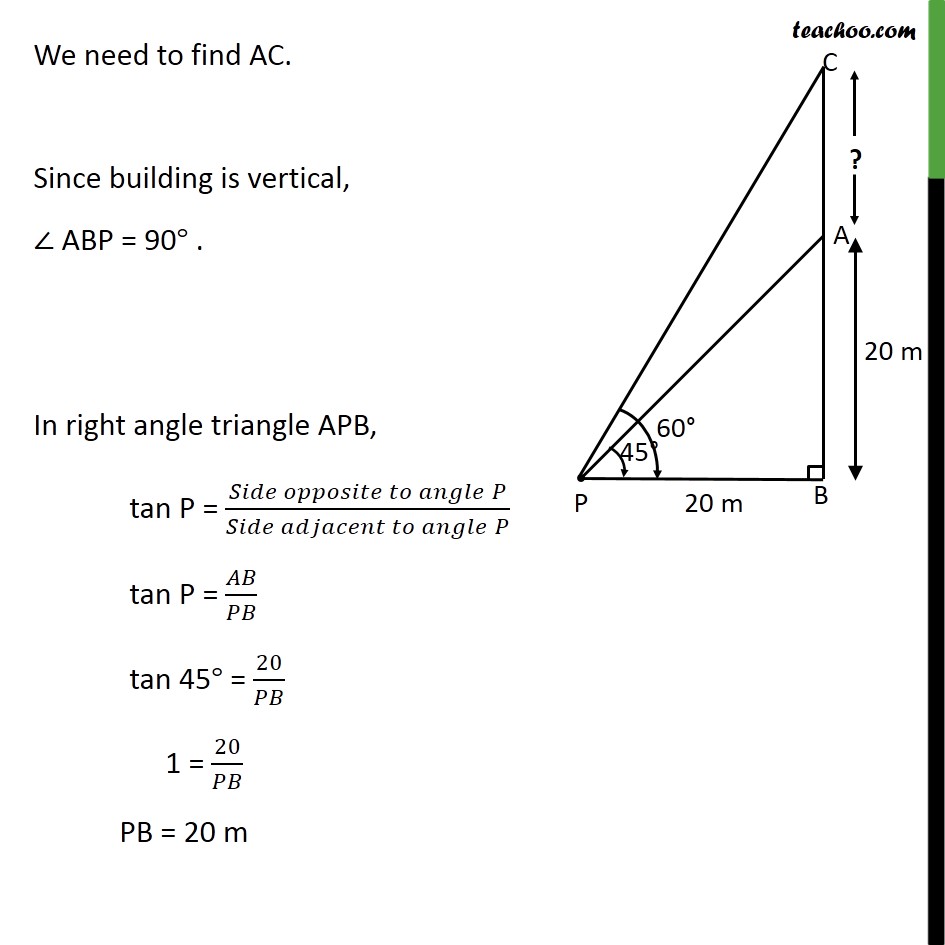
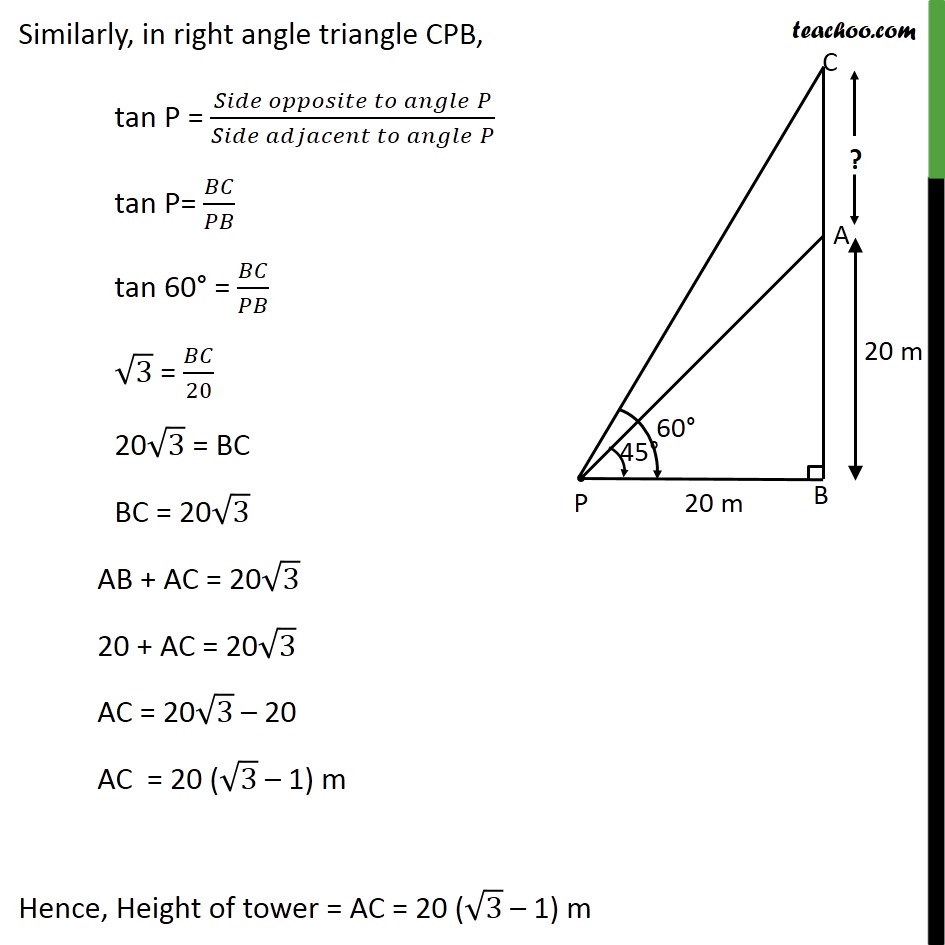
Ex 9.1 , 7 From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45 and 60 respectively. Find the height of the tower. Let the building be AB and tower be CA. Building is 20 m high, So, AB = 20m Let point of ground be P. Angle of elevation from point P to bottom of tower A = 45 Hence, APB = 45 Also, Angle of elevation from point P to top of the tower C = 60 Hence, CPB = 60 We need to find AC. Since building is vertical, ABP = 90 . In right angle triangle APB, tan P = ( " " )/( " " ) tan P = / tan 45 = 20/ 1 = 20/ PB = 20 m Similarly, in right angle triangle CPB, tan P = ( " " )/( " " ) tan P= / tan 60 = / 3 = /20 20 3 = BC BC = 20 3 AB + AC = 20 3 20 + AC = 20 3 AC = 20 3 20 AC = 20 ( 3 1) m Hence, Height of tower = AC = 20 ( 3 1) m

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.