Check sibling questions

Example 4 - Chapter 8 Class 10 Introduction to Trignometry

Last updated at May 29, 2023 by

Example 4 - If tan A = 1, then verify 2 sin A cos A = 1 - Proving

Example 4 - Chapter 8 Class 10 Introduction to Trignometry - Part 2
Example 4 - Chapter 8 Class 10 Introduction to Trignometry - Part 3

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

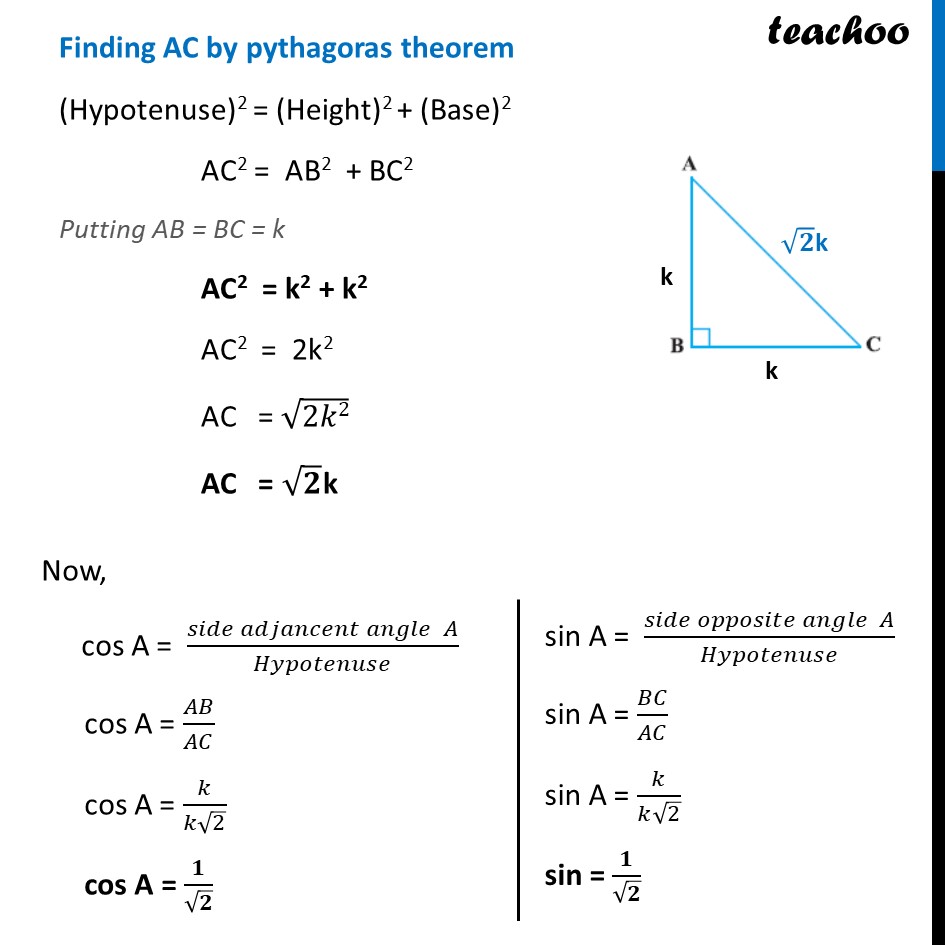
Example 4 In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1. Finding AC by pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 AC2 = AB2 + BC2 Putting AB = BC = k AC2 = k2 + k2 AC2 = 2k2 AC = √2π‘˜2 AC = k √2 We have to find 2 sin A cos A Substituting the value of sin A and cos A = 2 Γ—1/√2Γ—1/√2 = 2/(√2 Γ— √2) = 2/(√2 )^2 = 2/2 = 1

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.