What is value of sin 30?
What about cos 0?
and sin 0?
How do we remember them?
Let's learn how. We will discuss what are different values of sin, cos, tan, cosec, sec, cot at 0, 30, 45, 60 and 90 degrees and how to memorise them.
So, we have to fill this table
How to find the values?
To learn the table, we should first know how sin cos tan are related
We know that
- tan θ = sin θ/cosθ
- sec θ = 1/cos θ
- cosec θ = 1/sin θ
- cot θ = 1/cot θ
Now let us discuss different values
For sin
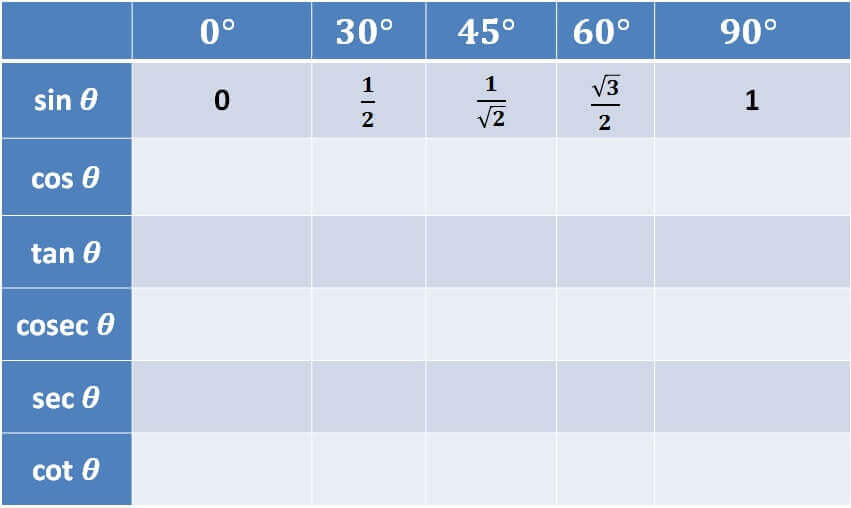
For memorising sin 0°, sin 30°, sin 45°, sin 60° and sin 90°
We should learn it like
- sin 0° = 0
- sin 30° = 1/2
- sin 45° = 1/√2
- sin 60° = √3/2
- sin 90° = 1
So, our pattern will be like
0, 1/2, 1/√2, √3/2, 1
For cos
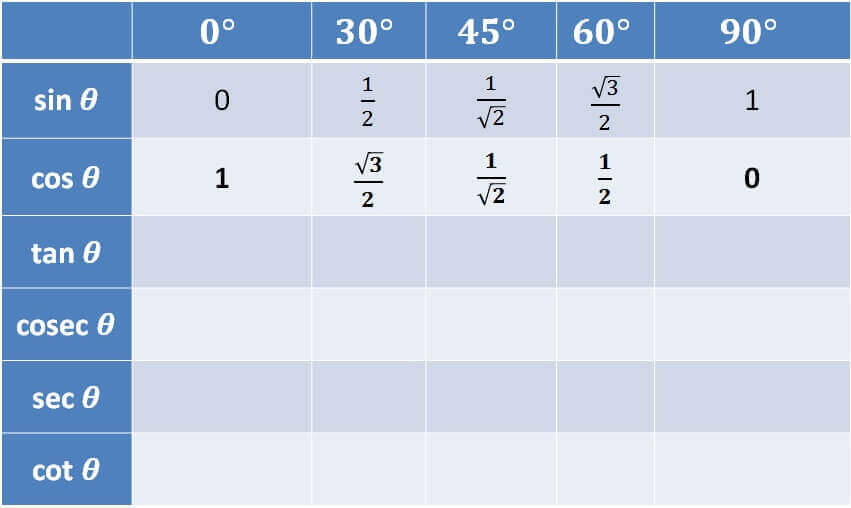
For memorising cos 0°, cos 30°, cos 45°, cos 60° and cos 90°
Cos is the opposite of sin.
We should learn it like
- cos 0° = sin 90° = 1
- cos 30° = sin 60° = √3/2
- cos 45° = sin 45° = 1/√2
- cos 60° = sin 30° = 1/2
- cos 90° = sin 0° = 0
So, for cos, it will be like
1, √3/2, 1/√2, 1/2, 0
For tan
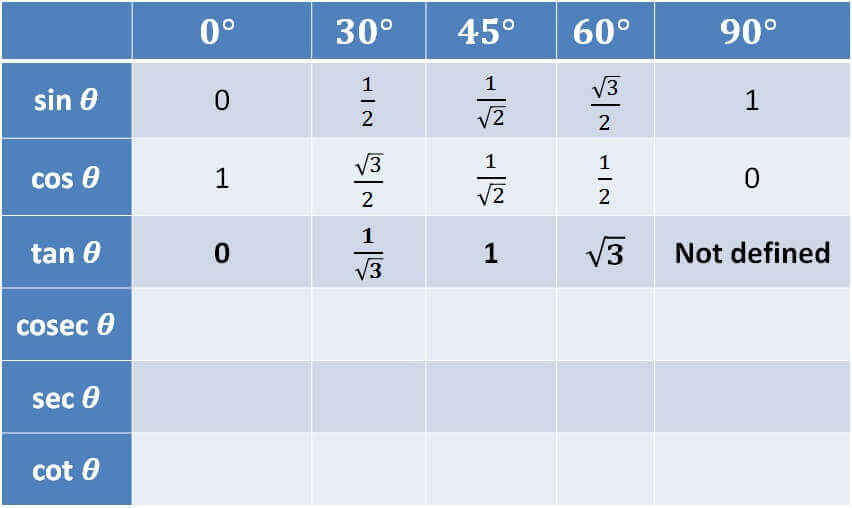
We know that tan θ = sin θ /cos θ
So, it will be
- tan 0° = sin 0° / cos 0° = 0/1 = 0
- tan 30° = sin 30° / cos 30° = (1/2)/ (√3/2) = 1/√3
- tan 45° = sin 45° / cos 45° = (1/√2)/ (1/√2) = 1
- tan 60° = sin 60° / cos 60° = (√3/2) / (1/2) = √3
- tan 90° = sin 90° / cos 90° = 1/0 = Not Defined = ∞
So, for tan, it is
0, 1/√3, 1, √3, ∞
For cosec
We know that
cosec θ = 1/sin θ
For sin, we know
0, 1/2, 1/√2, √3/2, 1
So, for cosec it will be
- cosec 0° = 1 / sin 0° = 1/0 = Not Defined = ∞
- cosec 30° = 1 / sin 40° = 1/(1/2) = 2
- cosec 45° = 1 / sin 45° = 1/(1/√2) = √2
- cosec 60° = 1 / sin 60° = 1/(√3/2) = 2/√3
- cosec 90° = 1 / sin 90° = 1/1 = 1
So, for cosec, it is
∞, 2, √2, 2/√3, 1
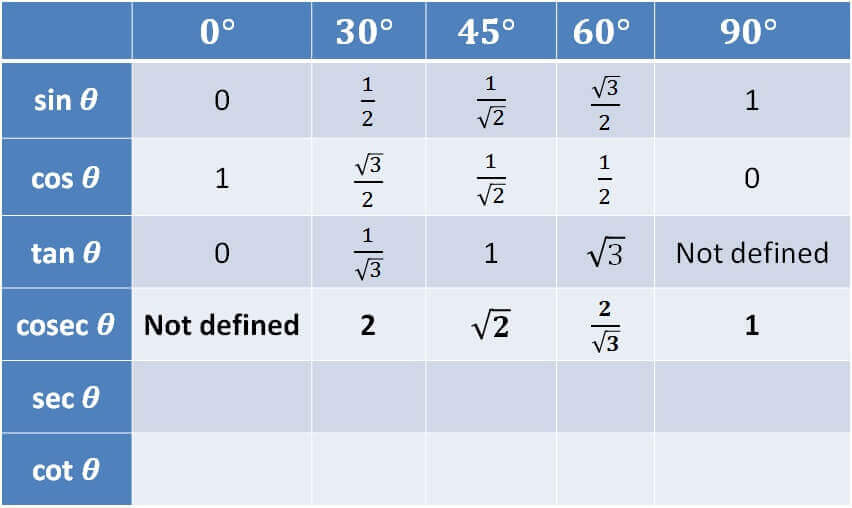
For sec
We know that
sec θ = 1/cos θ
For cos, we know
1, √3/2, 1/√2, 1/2, 0
So, for sec it will be
- sec 0° = 1 / cos 0° = 1/1 = 1
- sec 30° = 1 / cos 40° = 1/(√3/2) = 2/√3
- sec 45° = 1 / cos 45° = 1/(1/√2) = √2
- sec 60° = 1 / cos 60° = 1/(1/2) = 2
- sec 90° = 1 / cos 90° = 1/0 = Not Defined = ∞
So, for sec, it is
1, 2/√3, √2, 2, ∞
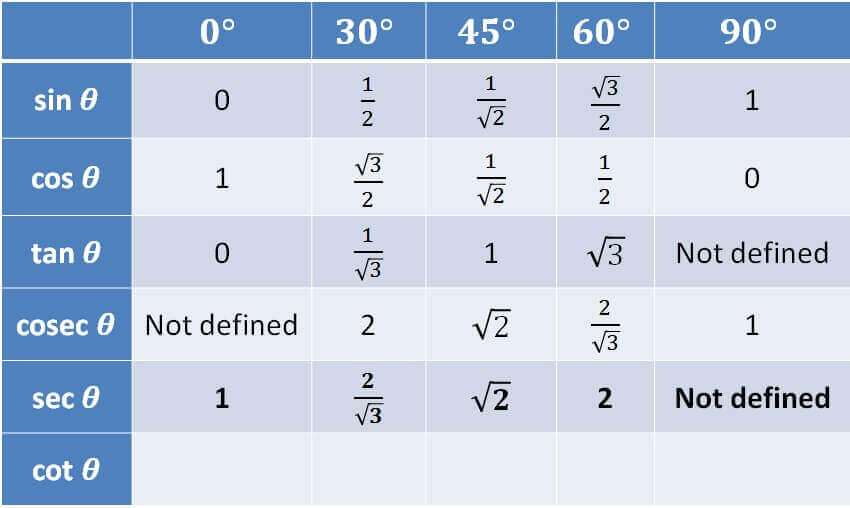
For cot
We know that
cot θ = 1/tan θ
For tan, we know that
0, 1/√3, 1, √3, ∞
So, for cot it will be
- cot 0° = 1 / tan 0° = 1/0 = Not Defined = ∞
- cot 30° = 1 / tan 30° = 1/(1/√3) = √3
- cot 45° = 1 / tan 45° = 1/1 = 1
- cot 60° = 1 / tan 60° = 1/√3
- cot 90° = 1 / tan 90° = 1/∞ = 0
So, for cot, it is
∞, √3, 1, 1/√3, 0
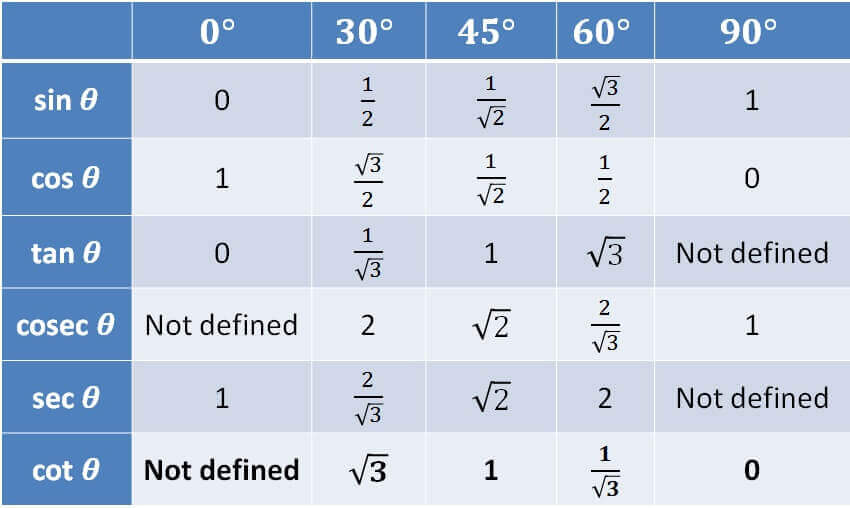
So, our full table looks like this
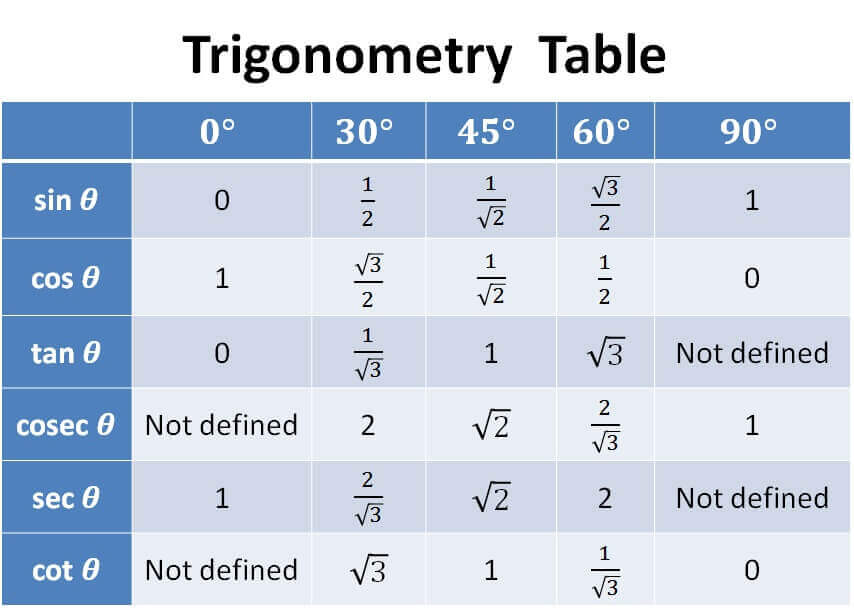
You can also practice questions by clicking Next.
Trigonometry Table
Trigonometry Table has all the values of sin, cos, tan for all angles from 0 to 90 degree.
You can also download it below
| Radian | Degree | Sine | Cosine | Tangent | Radian | Degree | Sine | Cosine | Tangent |
| 0.000 | 0 | 0.000 | 1.000 | 0.000 | 0.803 | 46 | 0.719 | 0.695 | 1.036 |
| 0.017 | 1 | 0.017 | 1.000 | 0.017 | 0.820 | 47 | 0.731 | 0.682 | 1.072 |
| 0.035 | 2 | 0.035 | 0.999 | 0.035 | 0.838 | 48 | 0.743 | 0.669 | 1.111 |
| 0.052 | 3 | 0.052 | 0.999 | 0.052 | 0.855 | 49 | 0.755 | 0.656 | 1.150 |
| 0.070 | 4 | 0.070 | 0.998 | 0.070 | 0.873 | 50 | 0.766 | 0.643 | 1.192 |
| 0.087 | 5 | 0.087 | 0.996 | 0.087 | 0.890 | 51 | 0.777 | 0.629 | 1.235 |
| 0.105 | 6 | 0.105 | 0.995 | 0.105 | 0.908 | 52 | 0.788 | 0.616 | 1.280 |
| 0.122 | 7 | 0.122 | 0.993 | 0.123 | 0.925 | 53 | 0.799 | 0.602 | 1.327 |
| 0.140 | 8 | 0.139 | 0.990 | 0.141 | 0.942 | 54 | 0.809 | 0.588 | 1.376 |
| 0.157 | 9 | 0.156 | 0.988 | 0.158 | 0.960 | 55 | 0.819 | 0.574 | 1.428 |
| 0.175 | 10 | 0.174 | 0.985 | 0.176 | 0.977 | 56 | 0.829 | 0.559 | 1.483 |
| 0.192 | 11 | 0.191 | 0.982 | 0.194 | 0.995 | 57 | 0.839 | 0.545 | 1.540 |
| 0.209 | 12 | 0.208 | 0.978 | 0.213 | 1.012 | 58 | 0.848 | 0.530 | 1.600 |
| 0.227 | 13 | 0.225 | 0.974 | 0.231 | 1.030 | 59 | 0.857 | 0.515 | 1.664 |
| 0.244 | 14 | 0.242 | 0.970 | 0.249 | 1.047 | 60 | 0.866 | 0.500 | 1.732 |
| 0.262 | 15 | 0.259 | 0.966 | 0.268 | 1.065 | 61 | 0.875 | 0.485 | 1.804 |
| 0.279 | 16 | 0.276 | 0.961 | 0.287 | 1.082 | 62 | 0.883 | 0.469 | 1.881 |
| 0.297 | 17 | 0.292 | 0.956 | 0.306 | 1.100 | 63 | 0.891 | 0.454 | 1.963 |
| 0.314 | 18 | 0.309 | 0.951 | 0.325 | 1.117 | 64 | 0.899 | 0.438 | 2.050 |
| 0.332 | 19 | 0.326 | 0.946 | 0.344 | 1.134 | 65 | 0.906 | 0.423 | 2.145 |
| 0.349 | 20 | 0.342 | 0.940 | 0.364 | 1.152 | 66 | 0.914 | 0.407 | 2.246 |
| 0.367 | 21 | 0.358 | 0.934 | 0.384 | 1.169 | 67 | 0.921 | 0.391 | 2.356 |
| 0.384 | 22 | 0.375 | 0.927 | 0.404 | 1.187 | 68 | 0.927 | 0.375 | 2.475 |
| 0.401 | 23 | 0.391 | 0.921 | 0.424 | 1.204 | 69 | 0.934 | 0.358 | 2.605 |
| 0.419 | 24 | 0.407 | 0.914 | 0.445 | 1.222 | 70 | 0.940 | 0.342 | 2.747 |
| 0.436 | 25 | 0.423 | 0.906 | 0.466 | 1.239 | 71 | 0.946 | 0.326 | 2.904 |
| 0.454 | 26 | 0.438 | 0.899 | 0.488 | 1.257 | 72 | 0.951 | 0.309 | 3.078 |
| 0.471 | 27 | 0.454 | 0.891 | 0.510 | 1.274 | 73 | 0.956 | 0.292 | 3.271 |
| 0.489 | 28 | 0.469 | 0.883 | 0.532 | 1.292 | 74 | 0.961 | 0.276 | 3.487 |
| 0.506 | 29 | 0.485 | 0.875 | 0.554 | 1.309 | 75 | 0.966 | 0.259 | 3.732 |
| 0.524 | 30 | 0.500 | 0.866 | 0.577 | 1.326 | 76 | 0.970 | 0.242 | 4.011 |
| 0.541 | 31 | 0.515 | 0.857 | 0.601 | 1.344 | 77 | 0.974 | 0.225 | 4.331 |
| 0.559 | 32 | 0.530 | 0.848 | 0.625 | 1.361 | 78 | 0.978 | 0.208 | 4.705 |
| 0.576 | 33 | 0.545 | 0.839 | 0.649 | 1.379 | 79 | 0.982 | 0.191 | 5.145 |
| 0.593 | 34 | 0.559 | 0.829 | 0.675 | 1.396 | 80 | 0.985 | 0.174 | 5.671 |
| 0.611 | 35 | 0.574 | 0.819 | 0.700 | 1.414 | 81 | 0.988 | 0.156 | 6.314 |
| 0.628 | 36 | 0.588 | 0.809 | 0.727 | 1.431 | 82 | 0.990 | 0.139 | 7.115 |
| 0.646 | 37 | 0.602 | 0.799 | 0.754 | 1.449 | 83 | 0.993 | 0.122 | 8.144 |
| 0.663 | 38 | 0.616 | 0.788 | 0.781 | 1.466 | 84 | 0.995 | 0.105 | 9.514 |
| 0.681 | 39 | 0.629 | 0.777 | 0.810 | 1.484 | 85 | 0.996 | 0.087 | 11.430 |
| 0.698 | 40 | 0.643 | 0.766 | 0.839 | 1.501 | 86 | 0.998 | 0.070 | 14.301 |
| 0.716 | 41 | 0.656 | 0.755 | 0.869 | 1.518 | 87 | 0.999 | 0.052 | 19.081 |
| 0.733 | 42 | 0.669 | 0.743 | 0.900 | 1.536 | 88 | 0.999 | 0.035 | 28.636 |
| 0.750 | 43 | 0.682 | 0.731 | 0.933 | 1.553 | 89 | 1.000 | 0.017 | 57.290 |
| 0.768 | 44 | 0.695 | 0.719 | 0.966 | 1.571 | 90 | 1.000 | 0.000 | ∞ |
| 0.785 | 45 | 0.707 | 0.707 | 1.000 |
Download in PDF
