Check sibling questions

Ex 8.2, 2 (i) (MCQ) - Chapter 8 Class 10 Introduction to Trignometry

Last updated at May 29, 2023 by

Ex 8.2, 2 (i) - Choose correct option - 2 tan 30 / 1 + tan^2 30 = (A) sin 60 (B) cos 60 (C) tan 60 (D) sin 30

Ex 8.2, 2 (i) - Chapter 8 Class 10 Introduction to Trignometry - Part 2

 

 

 

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

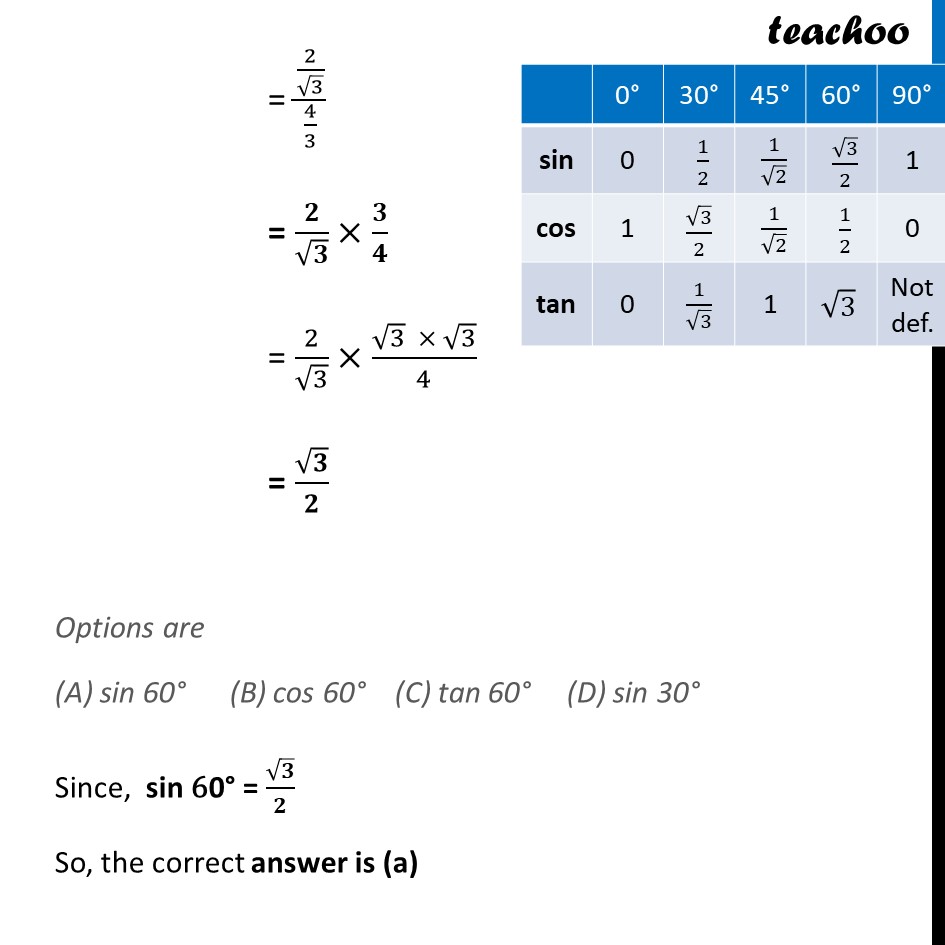
Ex 8.2, 2 Choose the correct option and justify your choice : (i) "2 tan 30 " /"1 + tan2 30 " = sin 60 (B) cos 60 (C) tan 60 (D) sin 30 We know that , tan "30 " = 1/ 3 So, (2 tan 30 )/(1+ 2 30 ) = (2 (1/ 3))/(1 + (1/ 3)^2 ) = (2/ 3)/(1 + 1/3) = (2/ 3)/(4/3) = 2/ 3 3/4 = 2/ 3 ( 3 3)/4 = 3/2 Options are (A) sin 60 (B) cos 60 (C) tan 60 (D) sin 30 Since sin "60 " = 3/2 Hence, option (A) is correct

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.