Ex 8.1, 7 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

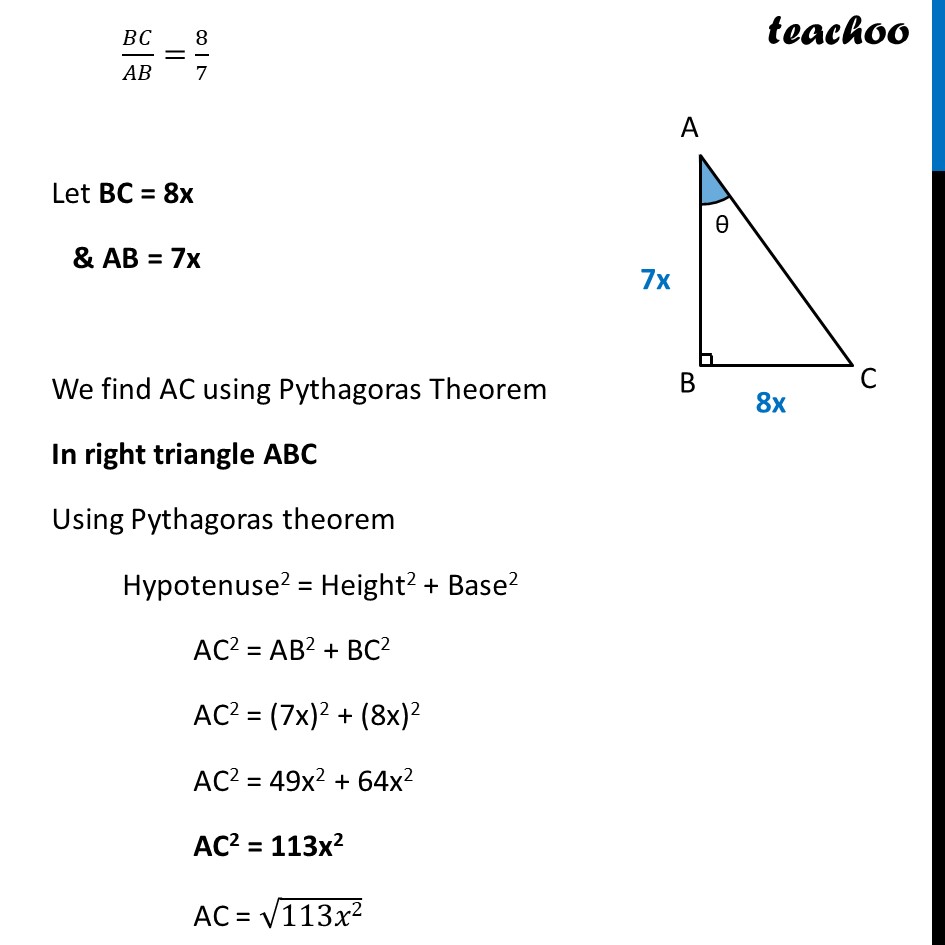
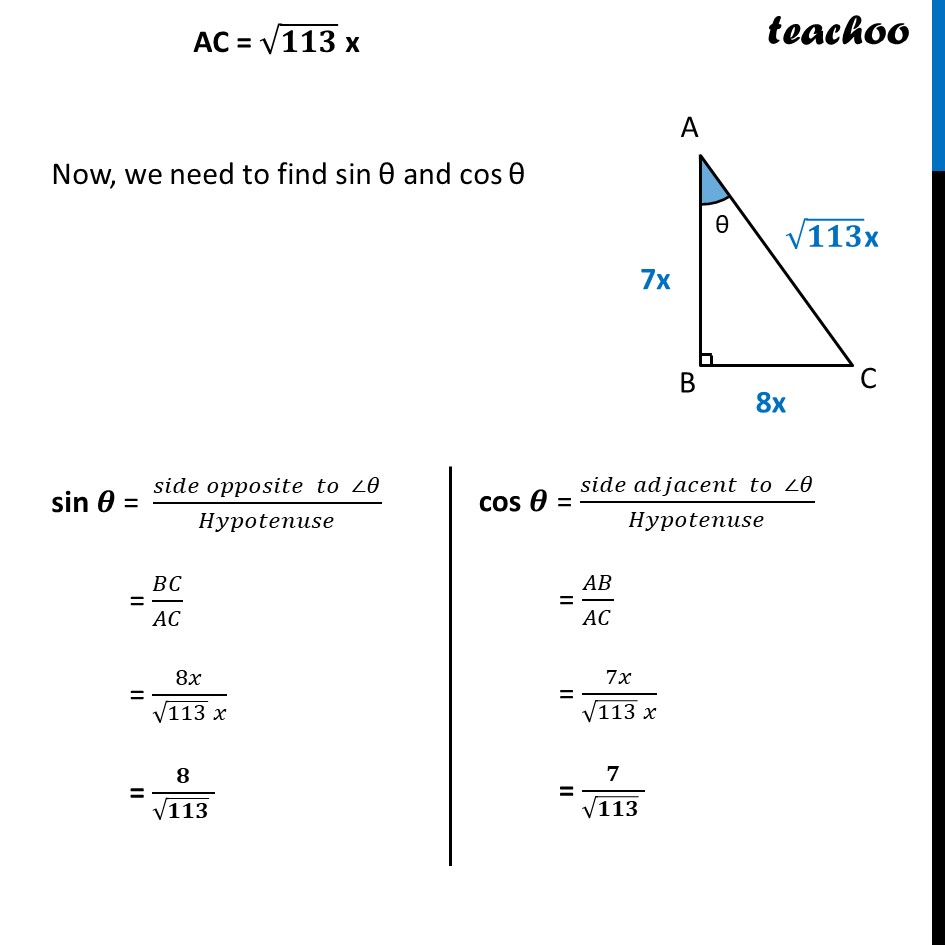
Ex 8.1, 7 If cot θ = 7/8 , evaluate : (i) ((1 + 𝑠𝑖𝑛⁡𝜃)(1 − 𝑠𝑖𝑛⁡𝜃))/((1 + 𝑐𝑜𝑠⁡𝜃)(1 − 𝑐𝑜𝑠⁡𝜃)) We will first calculate the value of sin θ & cos θ Now, tan θ = 1/cot⁡𝜃 tan θ = 1/(7/8) tan θ = 8/7 (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 ∠𝜃)/(𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 ∠𝜃)=8/7 𝐵𝐶/𝐴𝐵=8/7 Let BC = 8x & AB = 7x We find AC using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 AC2 = AB2 + BC2 AC2 = (7x)2 + (8x)2 AC2 = 49x2 + 64x2 AC2 = 113x2 AC = √113𝑥2 AC = √113 x Now, we need to find sin θ and cos θ sin 𝜃 = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝜃)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝐵𝐶/𝐴𝐶 = 8𝑥/(√113 𝑥) = 8/(√113 ) Here, We have to evaluate ((1 + sin⁡𝜃 ) (1 −〖 sin〗⁡𝜃 ))/((1 + cos⁡𝜃 ) (1 −〖 cos〗⁡𝜃 ) ) Using (a + b) (a – b) = a2 – b2 = ( (12 − 𝑠𝑖𝑛2 𝜃))/( (12 − 𝑐𝑜𝑠2𝜃)) = ( (1 − 𝑠𝑖𝑛2 𝜃))/( (1 − 𝑐𝑜𝑠2𝜃)) Putting sin 𝜃 = 8/(√113 ) & cos θ = 7/(√113 ) = ((1 − (8/(√113 ))^2 ))/((1 − (7/(√113 ))^2 ) ) = ((1 − 8^2/(√113)2))/((1 − 72/(√113)2) ) = ((1 − 64/113))/((1 − 49/113) ) = (((113 − 64)/113))/(((113 − 49)/113) ) = (113 − 64)/(113 − 49 ) = 49/(64 ) Hence, ((1 + 𝑠𝑖𝑛⁡𝜃)(1 − 𝑠𝑖𝑛⁡𝜃))/((1 + 𝑐𝑜𝑠⁡𝜃)(1 − 𝑐𝑜𝑠⁡𝜃)) = 49/(64 )