Ex 8.1, 4 - Chapter 8 Class 10 Introduction to Trignometry

Transcript

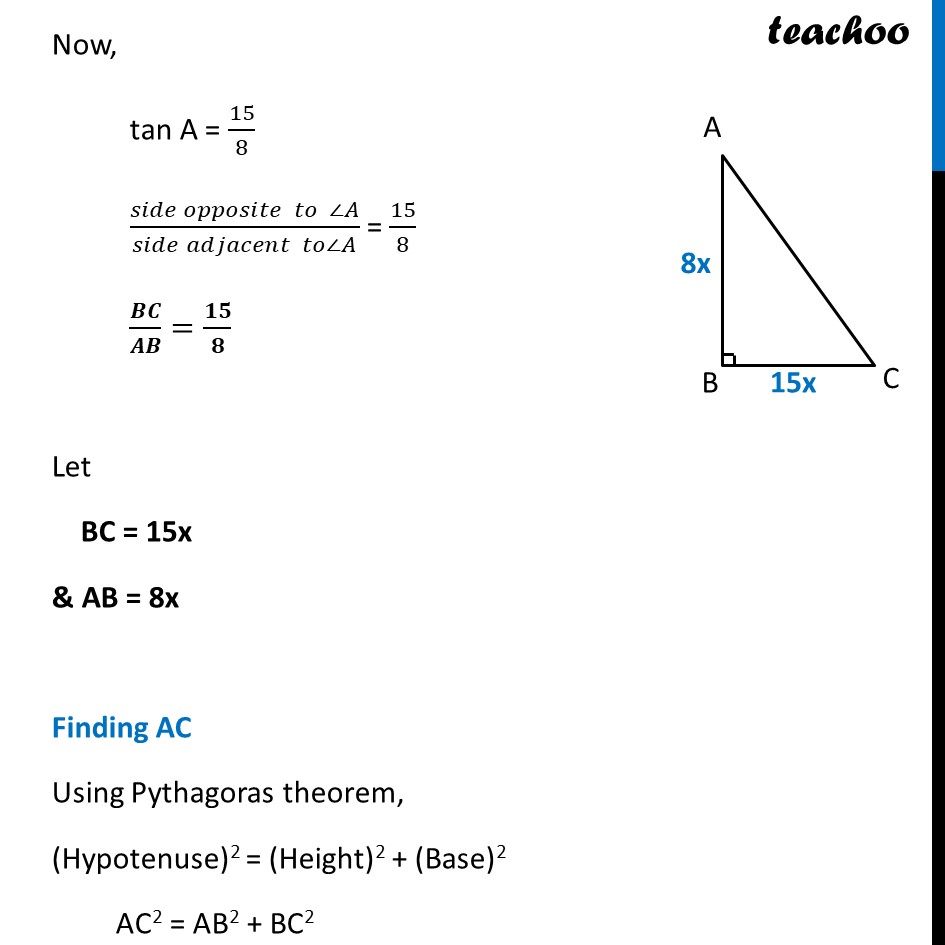
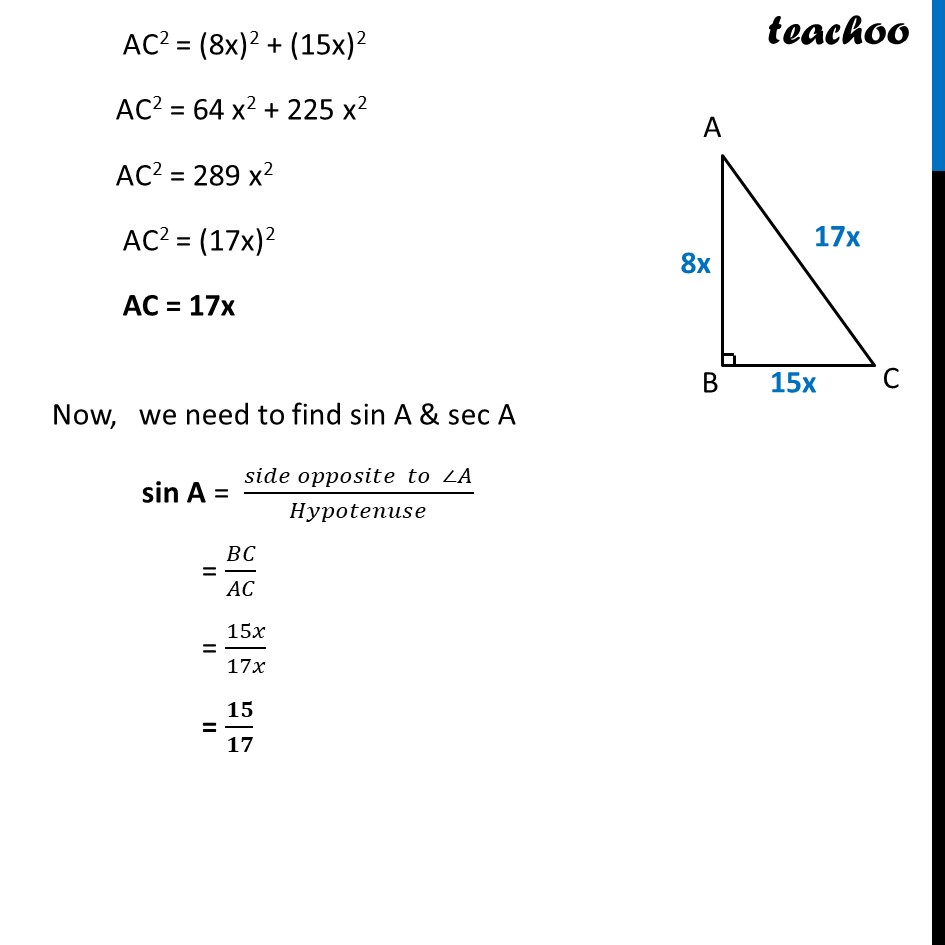
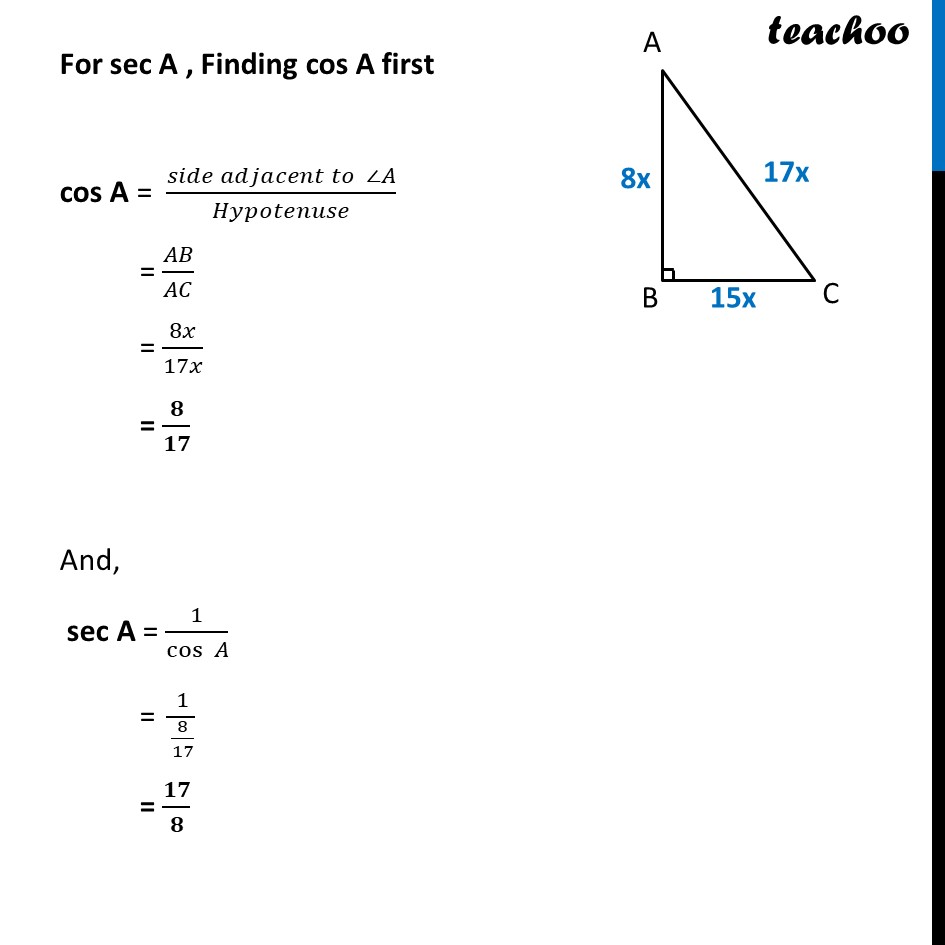
Ex 8.1, 4 Given 15 cot A = 8, find sin A and sec A. Given 15 cot A = 8 cot A = 𝟖/𝟏𝟓 Now, tan A = 1/cot⁡𝐴 = 1/(8/15) = 𝟏𝟓/𝟖 Now, tan A = 15/8 (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴)/(𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜∠𝐴) = 15/8 𝑩𝑪/𝑨𝑩=𝟏𝟓/𝟖 Let BC = 15x & AB = 8x Finding AC Using Pythagoras theorem, (Hypotenuse)2 = (Height)2 + (Base)2 AC2 = AB2 + BC2 AC2 = (8x)2 + (15x)2 AC2 = 64 x2 + 225 x2 AC2 = 289 x2 AC2 = (17x)2 AC = 17x Now, we need to find sin A & sec A sin A = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝐵𝐶/𝐴𝐶 = 15𝑥/17𝑥 = 𝟏𝟓/𝟏𝟕 For sec A , Finding cos A first cos A = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠𝐴)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝐴𝐵/𝐴𝐶 = 8𝑥/17𝑥 = 𝟖/𝟏𝟕 And, sec A = 1/cos⁡〖 𝐴〗 = 1/(8/17) = 𝟏𝟕/𝟖