Ex 7.3, 5 - Chapter 7 Class 10 Coordinate Geometry (Term 1)

Transcript

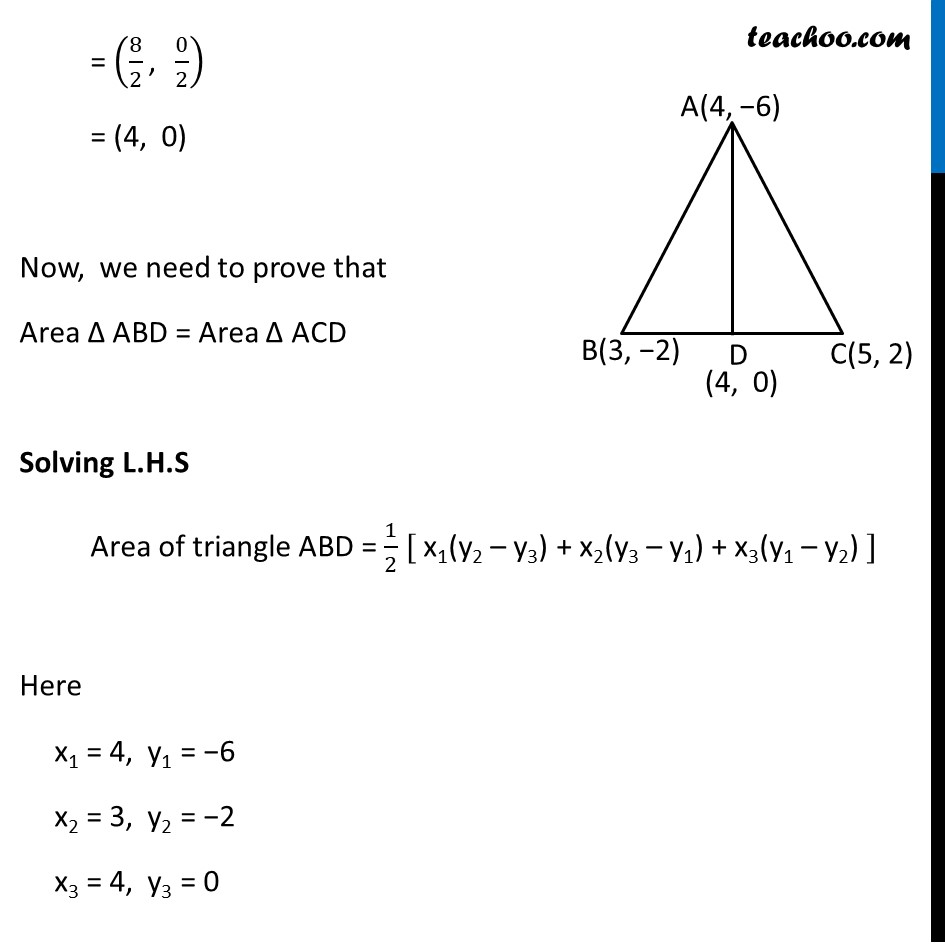
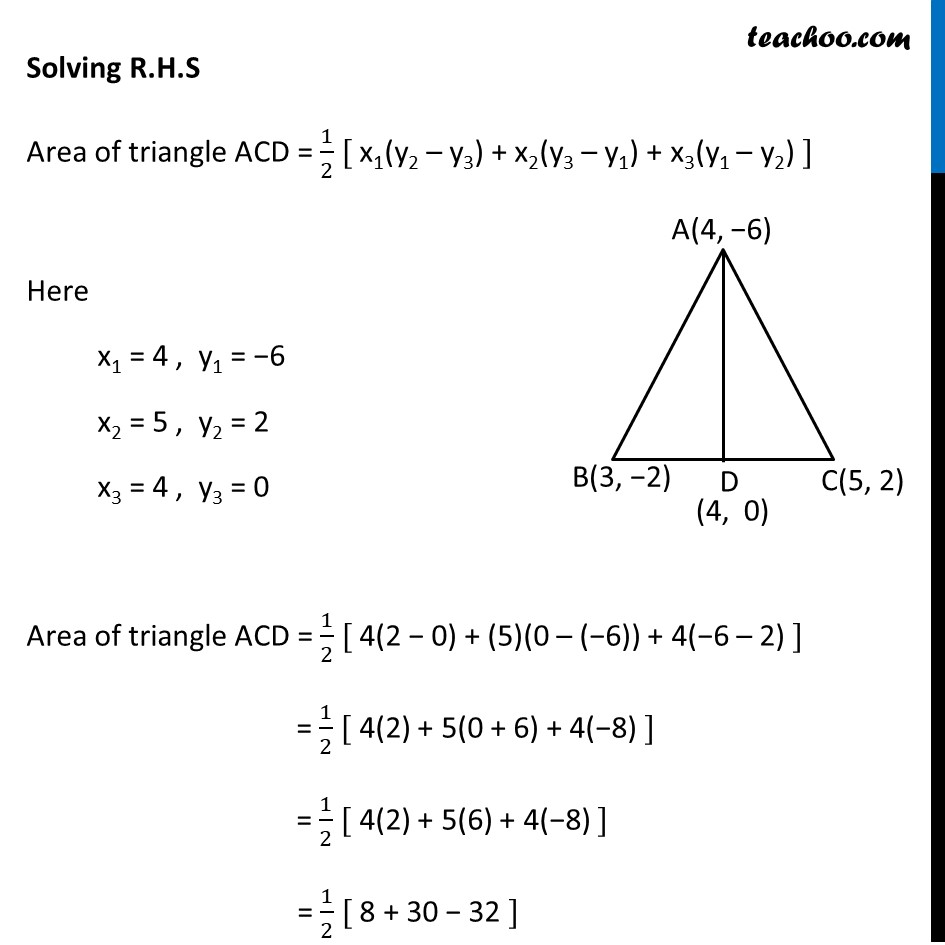
Ex 7.3 , 5 You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, – 6), B(3, –2) and C(5, 2) Let ∆ ABC be as shown in the figure Let AD be the median which divides BC into two equal parts, BD & CD Hence, Coordinates of D = ((𝑥1 + 𝑥2)/2 ", " (𝑦1 +𝑦2)/2) = ((3 + 5)/2 ", " (−2 + 2)/2) = (8/2 ", " 0/2) = (4, 0) Now, we need to prove that Area ∆ ABD = Area ∆ ACD Solving L.H.S Area of triangle ABD = 1/2 [ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) ] Here x1 = 4, y1 = −6 x2 = 3, y2 = −2 x3 = 4, y3 = 0 Putting values Area of triangle ABD = 1/2 [4(−2 − 0) + (3)(0 – (−6)) + 4(−6 – (−2))] = 1/2 [ 4(−2) + 3(0 + 6) + 4(−6 + 2)] = 1/2 [ 4(−2) + 3(6) + 4(−4)] = 1/2 [−8 + 18 −16] = 1/2 [−6] = −3 Now, since area cannot be negative Area of triangle ABC = 3 square units Solving R.H.S Area of triangle ACD = 1/2 [ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) ] Here x1 = 4 , y1 = −6 x2 = 5 , y2 = 2 x3 = 4 , y3 = 0 Area of triangle ACD = 1/2 [ 4(2 − 0) + (5)(0 – (−6)) + 4(−6 – 2) ] = 1/2 [ 4(2) + 5(0 + 6) + 4(−8) ] = 1/2 [ 4(2) + 5(6) + 4(−8) ] = 1/2 [ 8 + 30 − 32 ] = 1/2 [6] = 3 square units = R.H.S Hence, Area of ∆ ABD = Area of ∆ ACD Hence proved