Ex 4.3, 6 - Chapter 4 Class 10 Quadratic Equations (Term 2)

Transcript

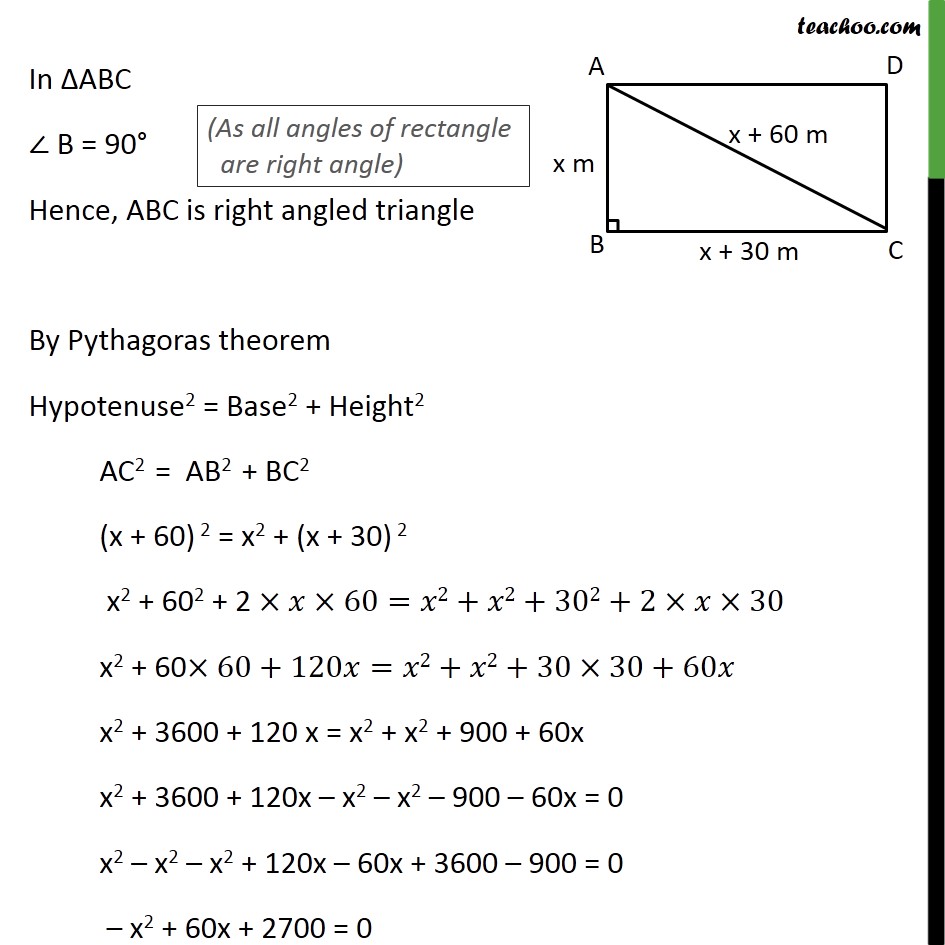
Ex 4.3 ,6 The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field. Let ABCD be the rectangular field AC is diagonal Let the shorter side = AB = x metres It is given that, Diagonal is 60 m more than shorter side AC = AB + 60 = x + 60 metres Also longer side is 30 m more than shorter side BC = AB + 30 = x + 30 metres In ABC B = 90 Hence, ABC is right angled triangle By Pythagoras theorem Hypotenuse2 = Base2 + Height2 AC2 = AB2 + BC2 (x + 60) 2 = x2 + (x + 30) 2 x2 + 602 + 2 60= 2+ 2+302+2 30 x2 + 60 60+120 = 2+ 2+30 30+60 x2 + 3600 + 120 x = x2 + x2 + 900 + 60x x2 + 3600 + 120x x2 x2 900 60x = 0 x2 x2 x2 + 120x 60x + 3600 900 = 0 x2 + 60x + 2700 = 0 0 = x2 60x 2700 x2 60x 2700 = 0 We factorize using splitting the middle term method x2 90x + 30x 2700 = 0 x (x 90) + 30 (x 90) = 0 (x + 30) (x 90) = 0 So, x = 30 and x = 90 are the roots of the equation Since x is the length , it cannot be negative So, x = 90 Shorter side of field = x = 90 metres & Longer side of field = x + 30 = 90 + 30 = 120 metres