Ex 8.2, 1 (iii) - Chapter 8 Class 10 Introduction to Trignometry

Transcript

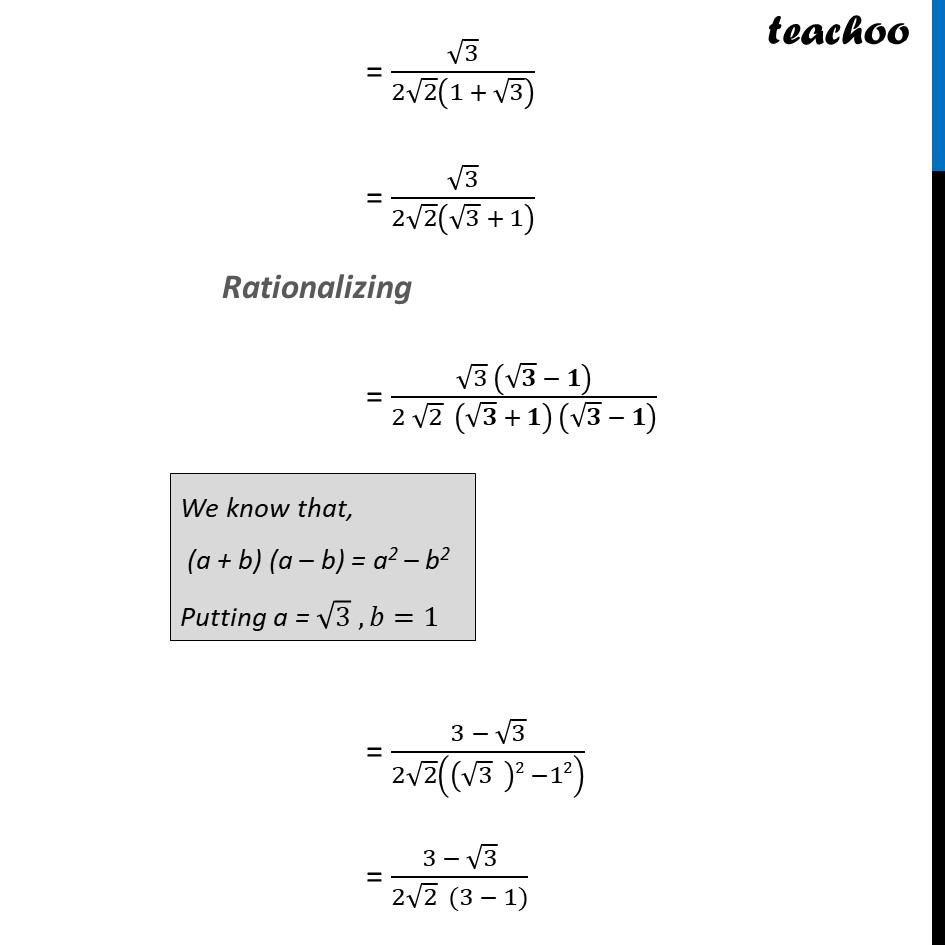
Ex 8.2, 1 Evaluate the following : (iii) "cos 45°" /"sec 30° + cosec 30°" We know that, "cos 45°" = 1/√2 "sec 30°" = 1/(cos⁡〖30°〗 ) = 1/(√3/2) = 𝟐/√𝟑 "cosec 30°" = 1/sin⁡〖30°〗 = 1/(1/2) = 2/1 = 2 Hence, 𝒄𝒐𝒔⁡〖𝟒𝟓°〗/(𝒔𝒆𝒄⁡〖𝟑𝟎°〗+ 𝒄𝒐𝒔𝒆𝒄 𝟑𝟎°) = (1/√2)/((2/√3 + 2/1) ) = 𝟏/√𝟐 × 𝟏/((𝟐/√𝟑 + 𝟐/𝟏) ) = 1/√2×1/((2 × 1 + 2 × √3)/(√3 × 1)) = 1/√2×(√3 × 1)/((2 × 1 + 2 × √3) ) = 𝟏/√𝟐×√𝟑/((𝟐 + 𝟐√𝟑) ) = (1 ×√3)/(√2 × 2(1 + √3) ) = √3/(2√2 (1 + √3) ) = √3/(2√2 (√3 + 1) ) Rationalizing = (√3 (√𝟑 − 𝟏))/(2 √2 (√𝟑 + 𝟏) (√𝟑 − 𝟏) ) We know that, (a + b) (a – b) = a2 – b2 Putting a = √3 , 𝑏=1 = (3 − √3)/(2√2 ((√3 )2 −12) ) = (3 − √3)/(2√2 (3 − 1)) = (𝟑 − √𝟑)/(𝟐√𝟐 × 𝟐) Multiplying √2 on numerator and denominator) = ((3 − √3 ))/(4√2 )× √2/√2 = (3√2 − √3 ×√2 )/(4 × 2) = (𝟑√𝟐 −√𝟔 )/𝟖 Hence, 𝒄𝒐𝒔⁡〖𝟒𝟓°〗/(𝒔𝒆𝒄⁡〖𝟑𝟎°〗+ 𝒄𝒐𝒔𝒆𝒄 𝟑𝟎°) = (𝟑√𝟐 −√𝟔 )/𝟖